What would it be like if the pivot was simply placed in that partition without a comparison? When I was teaching sorting algorithms, I used to work that way - pick a pivot, place it down in the middle of the desk, and physically place things to the left or right of it.
Though, when you’re sorting an array of 52 elements with four copies of each of the numbers from 1 to 13, even a stupidly bad pivot will still only take you a few steps 
I would hope instead that people find it close to the clearest 
.
The intuition underlying quicksort is simple and beautiful. As shown, if you implement it without trying to be “clever” about memory use, it’s naturally stable too.
Instead people get lost in the weeds of the horribly delicate end conditions for the “start at both ends and meet in the middle” memory-efficient partitioning code. People screw that up more often than they code a wrong binary search.
But that isn’t inherent to quicksort - just an artifact of aggressive implementation.
Then again, that aggressive code is key to qucksort’s greatest real-world strength: mergesort does substantially fewer compares on average, but “meet in the middel” quicksort does much less memory movement.
To stay sane I guess it is enough to protect up to json input. With full knowledge of the algorithm and ability to implement operators I am finding it difficult not to find a way how to screw things up if intended…
I had very similar one, but the one you shared improved upon it in few ways.
Been there twice already. Second one was just today - tried to improve upon my earlier in-place quicksort code, but just made it worse…
My latest version now:
def quick_sort_iter(arr):
from random import sample
if not isinstance(arr, (list, tuple)):
arr = list(arr)
q = [(False, arr)]
qappend = q.append
pop = q.pop
result = []
rns = None
while q:
is_sorted, arr = pop()
if arr:
if is_sorted:
yield from arr
elif (n := len(arr)) < 20:
if n == 1:
yield arr[0]
elif n == 2:
a, b = arr
if a <= b:
yield a
yield b
else:
yield b
yield a
else:
yield from sorted(arr)
else:
lt, eq, gt = [], [], []
lappend = lt.append
eappend = eq.append
gappend = gt.append
if rns is None:
rns = set()
add = rns.add
while len(rns) < 7:
add(int(random.random() * 1000))
rns = list(rns)
pivot = sorted([
arr[n * rns[0] // 1000],
arr[n * rns[1] // 1000],
arr[n * rns[2] // 1000],
arr[n * rns[3] // 1000],
arr[n * rns[4] // 1000],
arr[n * rns[5] // 1000],
arr[n * rns[6] // 1000]
])[3]
x_lt = _EMPTY
x_gt = _EMPTY
lt_sorted = 1
gt_sorted = 1
for x in arr:
if x < pivot:
if lt_sorted and x_lt is not _EMPTY and x < x_lt:
lt_sorted = 0
x_lt = x
lappend(x)
elif x > pivot:
if gt_sorted and x_gt is not _EMPTY and x < x_gt:
gt_sorted = 0
x_gt = x
gappend(x)
elif x is pivot or x == pivot:
eappend(x)
else:
raise ValueError('Malicious Data to sort')
if not eq:
raise ValueError('Malicious Data to sort')
qappend((gt_sorted, gt))
qappend((True, eq))
qappend((lt_sorted, lt))
return result
I believe that’s most-common practice now. The pivot is swapped into the first (or last) slice position at the start; partitioning proceeds as if that position didn’t exist; and then, at the end, the pivot is swapped into the “met at the middle” position and is excluded from further partitioning passes.
Algorithms that do that can’t be provoked into taking infinite time .
The code I posted, though, isn’t doing any in-place mutations, and has no idea what the index of the pivot may be (in order to swap it “out of the way” before partitioning starts).
It would work fine as-is if I did the is comparison first, but then that would slow the more typical cases where elements aren’t equal to the pivot.
It’s always something 
.
I propose a challenge. - “Perfect iterator sorting algorithm in Pure Python”.
Such would inevitably need to hold all of the data at initialisation.
Preconditions:
Goodness criteria:
sorted(arr). See below:Test cases:
def extend_list(arr, rep):
"""Extends inputted list in a repeating pattern..."""
if rep > 1:
n = len(arr)
diffs = [0] + [arr[i] - arr[i-1] for i in range(1, n)]
last = arr[-1]
for _ in range(rep):
for diff in diffs:
last = last + diff
arr.append(last)
return arr
M = 1000
l0 = list(range(10 * M))
l1 = l0[::-1]
l2 = extend_list([1, 0, 3, 2, 5, 4, 7, 6, 9, 8], M)
l3 = l2[::-1]
l4 = [54, 26, 93, 17, 77, 31, 44, 55, 20] * M
l5 = [20, 30, 40, 90, 50, 60, 70, 80, 100, 110] * M
random.seed(100)
l6 = [random.randint(0, M) for _ in range(10 * M)]
cases = [l0, l1, l2, l3, l4, l5, l6]
cases = [[[i] for i in c] for c in cases]
So @tim.one 's recipe is quite nice. Used a slightly modified version of it.
However, it’s initialisation time is still a bit too large:
random.seed(1000)
M = 100_000
RANDOM = list(zip([random.randint(0, M // 10) for _ in range(M)]))
sort_iter = heapsort_iter
assert all(map(opr.is_, sorted(RANDOM), sort_iter(RANDOM)))
%timeit sorted(RANDOM) # 48 ms
%timeit next(sort_iter(RANDOM)) # 18 ms
%timeit list(sort_iter(RANDOM)) # 160 ms
So full sort via sorted is 48ms, while getting the first element under iterator version is 18ms.
“The obvious” way using a heap is O()-optimal for minimizing time to first result. Someone could “cheat” by yielding min(arr) first thing, and it’s impossible to do anything faster than that (n-1 compares are necessary and sufficient to find the smallest). That’s linear-time, but so is heapify(arr). After heapifying, just keep popping and yielding one at a time. Worst, best, and expected cases all O(n log n).
Do you care about stability (it wasn’t mentioned)? The quicksort-based version I posted was stable, despite that “everyone says” quicksort isn’t stable .
That’s possible with a heapsort-based version too, but not “naturally” so. Instead of pushing elements on to the heap, push (element, original_index) two-tuples. Then element value ties are resolved in favor of the element with the smaller index, preserving stability.
To be very clear, here’s the total code needed to do an O() optimal job. Close to trivial to write!
from heapq import heapify, heappop
def isorted_heap(xs):
# decorate each element with its index, to ensure stability
xs = [t[::-1] for t in enumerate(xs)]
heapify(xs)
while xs:
yield heappop(xs)[0]
But sorting with a heap is generally far from the fastest way for total time.
I hope people will be motivated by the challenge of finding a good algorithm as opposed to “winning”. At least this is my intent now.
Yes, it should be stable!
I think people say that quicksort is unstable, because “holy grail” is supposedly O(1) and such quicksort is unstable (or at least very complex). O(1) quicksort is already a headache without stability…
Slow… At least by using heapq from SL.
random.seed(1000)
M = 100_000
RANDOM = list(zip([random.randint(0, M // 10) for _ in range(M)]))
sort_iter = heapsort_iter
assert all(map(opr.is_, sorted(RANDOM), sort_iter(RANDOM)))
%timeit sorted(RANDOM) # 55 ms
%timeit next(sort_iter(RANDOM)) # 45 ms
%timeit list(sort_iter(RANDOM)) # 346 ms
def heapsort_iter(arr):
"""
Examples:
>>> list(heapsort_iter([0, 1, 2, 3]))
[0, 1, 2, 3]
>>> data = list(zip([10, 10, 4, 4, 10, 10, 3, 2, 1]))
>>> all(map(opr.is_, heapsort_iter(data), sorted(data)))
True
"""
arr = list(zip(arr, itl.count()))
heapq.heapify(arr)
return map(opr.itemgetter(0), map(heapq.heappop, itl.repeat(arr, len(arr))))
As opposed to slightly modified stable quicksort you shared earlier:
assert all(map(opr.is_, sorted(RANDOM), sort_iter(RANDOM)))
%timeit sorted(RANDOM) # 48 ms
%timeit next(sort_iter(RANDOM)) # 18 ms
%timeit list(sort_iter(RANDOM)) # 160 ms
Note1: Updated test cases to list(zip(case)). This is to implicitly test for stability via operator.is_.
Note2: Also updated preconditions and goodness criteria.
Popping in to note a possible surprise: all these kinds of things run slower under PyPy than under CPython. Even plain old min(a_list) runs slower under PyPy.
I’ve bumped into this before, and believe I know the cause: when list elements are simple scalar types (chiefly floats and <= 64-bit signed ints), PyPy gets to close to native machine speed on compares. But when they’re fancier, it can lose instead.
In the current iteration of experiments, @Stefan2 started wrapping list element in 1-lists, and you’re wrapping them in 1-tuples, as clever ways of using object identity to verify results are “stable”. But then we’re doing lexicographic container comparisons instead at the top level, and PyPy is kneecapped.
Doesn’t CPython’s sort optimize this way for ints / floats? (similarly to how sum does)
Pretty much. CPython’s sort avoids the high expense of full-blown PyObject_RichCompareBool() for a list containing objects of the same type, no matter what it is. For floats and “small enough” ints, it also specializes to much faster close-to-machine compares. Although it takes a linear-time pre-pass over the list first to detect when it can do that.
But PyPy is fancier. Because it doesn’t have a C API to worry about, it’s free to use any number of concrete types for list under the covers, and for lists it can detect hold floats and “small enough” ints it stores the raw machine bits directly - no “objects” involved.
CPython can’t do that. No matter how small an int, our sort still has to deal with “int objjects”, and every compare still needs to build machine ints out of the Python int objects wrapping them. That’s pretty cheap, but not free The biggest expense is that CPython stores ints in sign+magnitude format, which has to be converted to native format (almost certainly 2’s-complement these days).
It could go on, e.g., to detect when a list holds only non-negative ints, and use an even faster comparison function to exploit that. But why bother ?
Then I think it is fair to test this with wrapped objects - this way it will be comparable to sorted, which will also have to do PyObject_RichCompareBool.
I wasn’t objecting to anything, just noting a possible surprise. Apples to apples is always best.
Note that, no, CPython isn’t reduced to PyObject_RichCompareBool even with the wrapping. A list of any homogeneous type gets some benefit.
“Your” way of wrapping is friendlier to the implementation than Stefan’s. CPython’s sort also specializes compare for lists of tuples where the tuples are all non-empty and their first elements are of the same type. It doesn’t do that for lists of lists, though.
Then I am amending test cases to use lists.
My tests are now going to look better.
I perhaps should’ve used 1-tuples (simply using zip as I usually do). I used lists only to be completely sure that Python doesn’t somehow optimize by reusing tuples for equal numbers, which would defeat the stability test.
Couple of graphs.
These are runtimes of each iteration.
First spike is initialisation.
This is for random data.
@tim.one’s recipe with minor edits.
Another graph:
isorted_sorted doesn’t fulfill the condition to “release returned values as soon as possible”.isorted_merge, but that’s terribly slow anyway, just included for fun for its brevity.from time import perf_counter as time
from itertools import *
from heapq import heapify, heappop, merge
from random import seed, random, randrange
from operator import itemgetter, is_not
def isorted_sorted(xs):
return iter(sorted(xs))
def isorted_heap_unstable(xs):
heap = list(xs)
heapify(heap)
return map(heappop, repeat(heap, len(heap)))
def isorted_heap_unstable_gen(xs):
heap = list(xs)
heapify(heap)
while heap:
yield heappop(heap)
def isorted_heap_stable(xs):
heap = list(zip(xs, count()))
heapify(heap)
return map(itemgetter(0), map(heappop, repeat(heap, len(heap))))
def isorted_heap_stable_gen(xs):
heap = list(zip(xs, count()))
heapify(heap)
while heap:
yield heappop(heap)[0]
def isorted_merge(xs):
return merge(*zip(xs))
def isorted_merge_batches_20(arr):
def batches():
for batch in batched(arr, 20):
batch = sorted(batch)
batch.reverse()
yield map(
list.pop,
repeat(batch, len(batch))
)
return merge(*batches())
def isorted_merge_batches_1000(arr):
def batches():
for batch in batched(arr, 1000):
batch = sorted(batch)
batch.reverse()
yield map(
list.pop,
repeat(batch, len(batch))
)
return merge(*batches())
def medianof3(x, y, z):
if y < x:
x, y = y, x
if z < y:
return x if z < x else z
else:
return y
def isorted_quicksort_stable(xs):
from random import sample
stack = [(False, list(xs))]
while stack:
alleq, xs = stack.pop()
if alleq:
yield from xs
continue
if len(xs) < 20:
yield from sorted(xs)
continue
lt = []
eq = []
gt = []
pivs = sample(xs, 9)
pivot = medianof3(medianof3(*pivs[0:3]),
medianof3(*pivs[3:6]),
medianof3(*pivs[6:9]))
for x in xs:
if x < pivot:
target = lt
elif x is pivot or x == pivot:
target = eq
else:
target = gt
target.append(x)
stack.append((False, gt))
stack.append((True, eq))
stack.append((False, lt))
funcs = [
isorted_sorted,
isorted_heap_unstable,
# isorted_heap_unstable_gen,
isorted_heap_stable,
# isorted_heap_stable_gen,
isorted_merge,
isorted_merge_batches_20,
isorted_merge_batches_1000,
isorted_quicksort_stable,
]
############################################################
# Correctness
############################################################
def correctness():
xs = [[randrange(10**4)] for _ in range(10**5)]
expect = sorted(xs)
for f in funcs:
result = list(f(iter(xs)))
if result != expect:
raise Exception(f'{f.__name__} failed to sort')
elif 'unstable' not in f.__name__ and any(map(is_not, result, expect)):
raise Exception(f'{f.__name__} is unstable and not declared as such')
correctness()
############################################################
# Speed
############################################################
# Assign None to rerun
times = {'isorted_sorted': [23.02, 23.04, 23.06, 23.07, 23.08, 23.09, 23.11, 23.13, 23.14, 23.15, 23.16, 23.17, 23.19, 23.2, 23.21, 23.22, 23.23, 23.25, 23.26, 23.27, 23.28, 23.3, 23.31, 23.32, 23.33, 23.34, 23.35, 23.37, 23.39, 23.4, 23.41, 23.43, 23.44, 23.45, 23.46, 23.48, 23.49, 23.5, 23.51, 23.52, 23.53, 23.55, 23.56, 23.57, 23.59, 23.61, 23.62, 23.64, 23.65, 23.66, 23.67, 23.68, 23.69, 23.71, 23.72, 23.73, 23.74, 23.75, 23.76, 23.78, 23.79, 23.8, 23.81, 23.84, 23.85, 23.86, 23.88, 23.89, 23.9, 23.91, 23.92, 23.93, 23.94, 23.95, 23.97, 23.98, 24.0, 24.01, 24.02, 24.03, 24.04, 24.06, 24.07, 24.08, 24.09, 24.11, 24.12, 24.14, 24.15, 24.16, 24.17, 24.18, 24.19, 24.21, 24.22, 24.23, 24.24, 24.25, 24.26, 24.27, 24.28], 'isorted_heap_unstable': [4.96, 5.79, 6.62, 7.39, 8.13, 8.84, 9.56, 10.23, 10.97, 11.64, 12.32, 13.0, 13.69, 14.52, 15.23, 15.93, 16.77, 17.54, 18.42, 19.17, 19.91, 20.69, 21.52, 22.41, 23.2, 24.01, 24.73, 25.41, 26.29, 27.07, 27.8, 28.57, 29.28, 29.94, 30.77, 31.45, 32.1, 32.75, 33.38, 34.05, 34.81, 35.46, 36.2, 36.91, 37.58, 38.18, 38.77, 39.37, 39.94, 40.54, 41.1, 41.78, 42.37, 42.94, 43.52, 44.1, 44.68, 45.23, 45.79, 46.39, 46.96, 47.57, 48.12, 48.75, 49.38, 49.97, 50.61, 51.43, 52.07, 52.68, 53.22, 53.78, 54.36, 54.91, 55.47, 55.97, 56.46, 56.95, 57.47, 58.03, 58.58, 59.06, 59.53, 59.99, 60.5, 60.94, 61.36, 61.75, 62.12, 62.5, 62.86, 63.22, 63.6, 63.96, 64.32, 64.7, 65.1, 65.64, 66.16, 66.67, 67.03], 'isorted_heap_stable': [31.04, 33.97, 36.48, 39.13, 41.77, 44.41, 47.07, 49.73, 52.28, 54.91, 57.39, 59.74, 62.1, 64.56, 66.91, 69.28, 71.58, 73.95, 76.35, 78.72, 81.26, 83.7, 86.13, 88.76, 91.22, 93.73, 96.18, 99.24, 101.77, 104.34, 106.84, 109.34, 111.76, 114.21, 116.76, 119.37, 121.88, 124.33, 126.57, 129.0, 131.4, 133.84, 136.18, 138.47, 140.69, 143.1, 145.34, 147.55, 149.86, 152.15, 154.34, 156.6, 158.87, 161.27, 163.52, 165.7, 167.88, 170.03, 172.14, 174.19, 176.23, 178.4, 180.66, 182.89, 184.96, 187.02, 189.01, 191.04, 192.89, 194.86, 196.88, 199.03, 201.18, 203.22, 205.24, 207.32, 209.19, 211.02, 212.8, 214.57, 216.4, 218.05, 219.76, 221.37, 222.96, 224.5, 225.99, 227.4, 228.86, 230.28, 231.51, 232.72, 233.83, 235.03, 236.21, 237.23, 238.18, 239.05, 239.83, 240.56, 241.17], 'isorted_merge': [6.14, 117.88, 122.89, 127.74, 133.11, 138.52, 143.89, 148.92, 153.79, 158.49, 163.48, 168.51, 173.37, 178.34, 183.27, 188.21, 193.12, 197.98, 202.93, 207.8, 212.7, 217.67, 222.37, 227.36, 232.52, 237.73, 242.8, 247.7, 252.52, 257.52, 262.3, 267.1, 271.8, 276.79, 281.85, 286.99, 292.68, 297.6, 302.8, 308.0, 312.99, 317.94, 323.03, 327.68, 332.2, 337.3, 342.59, 347.65, 352.54, 357.66, 362.78, 367.58, 372.37, 377.17, 381.85, 386.64, 391.29, 396.14, 400.95, 405.57, 410.07, 414.47, 418.74, 423.13, 427.59, 432.3, 437.03, 442.22, 446.91, 451.46, 456.07, 460.51, 464.75, 468.88, 472.85, 477.0, 481.16, 485.24, 489.73, 493.95, 498.02, 502.12, 506.14, 510.03, 513.91, 517.65, 521.42, 525.27, 528.97, 532.61, 536.07, 539.46, 542.99, 546.31, 549.5, 552.52, 555.31, 557.96, 560.44, 562.34, 564.05], 'isorted_merge_batches_20': [18.17, 23.06, 24.47, 25.88, 27.22, 28.53, 29.97, 31.57, 33.01, 34.4, 36.07, 37.49, 38.91, 40.25, 41.55, 42.85, 44.26, 45.68, 47.09, 48.57, 50.04, 51.61, 53.15, 54.68, 56.2, 57.88, 59.67, 61.27, 63.19, 64.94, 66.7, 68.57, 70.3, 72.04, 73.64, 75.14, 76.62, 78.2, 79.78, 81.28, 82.77, 84.35, 85.92, 87.68, 89.23, 90.65, 92.09, 93.48, 94.98, 96.42, 97.92, 99.45, 100.93, 102.45, 103.94, 105.5, 107.09, 108.58, 109.99, 111.37, 113.33, 115.02, 116.52, 118.26, 119.82, 121.32, 122.86, 124.43, 126.0, 127.52, 129.05, 130.54, 132.43, 134.19, 135.73, 137.28, 139.08, 140.66, 142.2, 143.75, 145.18, 146.65, 148.32, 149.86, 151.49, 153.19, 155.04, 156.9, 158.63, 160.49, 162.41, 164.21, 166.03, 167.77, 169.57, 171.48, 173.3, 174.98, 176.46, 177.87, 179.32], 'isorted_merge_batches_1000': [13.54, 14.32, 15.05, 15.69, 16.32, 17.05, 17.64, 18.29, 18.9, 19.5, 20.11, 20.69, 21.28, 21.91, 22.48, 23.05, 23.62, 24.22, 24.96, 25.55, 26.14, 26.78, 27.36, 27.93, 28.52, 29.12, 29.88, 30.46, 31.04, 31.63, 32.25, 32.85, 33.45, 34.04, 34.64, 35.31, 35.9, 36.56, 37.28, 37.92, 38.51, 39.19, 39.86, 40.49, 41.1, 41.85, 42.5, 43.14, 43.71, 44.36, 45.03, 45.64, 46.23, 46.97, 47.58, 48.17, 48.8, 49.39, 50.01, 50.59, 51.19, 51.81, 52.39, 52.96, 53.59, 54.19, 54.77, 55.44, 56.16, 56.87, 57.47, 58.07, 58.68, 59.26, 59.84, 60.47, 61.05, 61.68, 62.3, 62.88, 63.53, 64.1, 64.67, 65.28, 65.9, 66.57, 67.22, 67.83, 68.43, 69.01, 69.58, 70.2, 70.79, 71.37, 72.05, 72.75, 73.35, 74.02, 74.63, 75.38, 76.12], 'isorted_quicksort_stable': [0.23, 22.01, 23.96, 25.16, 26.49, 27.55, 28.71, 30.23, 31.33, 34.16, 35.14, 36.58, 37.66, 38.78, 41.19, 42.5, 43.51, 44.6, 45.93, 49.66, 50.7, 51.76, 53.23, 54.53, 55.48, 56.93, 58.01, 60.28, 61.33, 62.29, 63.56, 68.35, 69.37, 70.29, 71.55, 73.32, 74.68, 75.73, 76.92, 80.76, 81.84, 82.9, 84.49, 85.71, 86.83, 90.76, 91.88, 93.61, 94.59, 95.89, 97.04, 98.94, 100.68, 101.63, 102.98, 103.93, 104.91, 115.58, 116.77, 117.92, 119.44, 120.5, 122.5, 123.42, 124.79, 125.67, 127.99, 129.07, 130.42, 131.46, 133.23, 134.29, 135.28, 137.65, 138.6, 139.75, 141.5, 142.56, 143.84, 145.05, 147.68, 148.86, 150.95, 152.6, 153.92, 155.08, 156.31, 159.99, 161.1, 162.4, 163.54, 164.63, 166.15, 167.14, 169.53, 170.69, 172.32, 174.17, 175.47, 176.55, 177.59]}
def benchmark():
seed(1000)
xs = [random() for _ in range(10**5)]
times = {f: [1e999] for f in funcs}
for _ in range(10):
for f in funcs:
ixs = iter(xs)
t0 = time()
it = f(ixs)
ts = [time() - t0]
for _ in range(100):
next(islice(it, 1000, 0), None)
ts.append(time() - t0)
times[f] = min(times[f], ts, key=lambda ts: ts[-1])
return {f.__name__: [round(t * 1e3, 2) for t in ts] for f, ts in times.items()}
if not times:
times = benchmark()
print(times)
############################################################
# Plot
############################################################
import matplotlib.pyplot as plt
x = range(101)
for name, y in times.items():
plt.plot(x, y, label=name)
plt.ylim(0, 200)
plt.title('isorting [random() for _ in range(10**5)]', weight='bold')
plt.xlabel('percent iterated', weight='bold')
plt.ylabel('time in milliseconds', weight='bold')
plt.legend(loc='upper left')
plt.savefig('isorted.png', dpi=200)
Nice plot! Thanks
Added 3 - all stable:
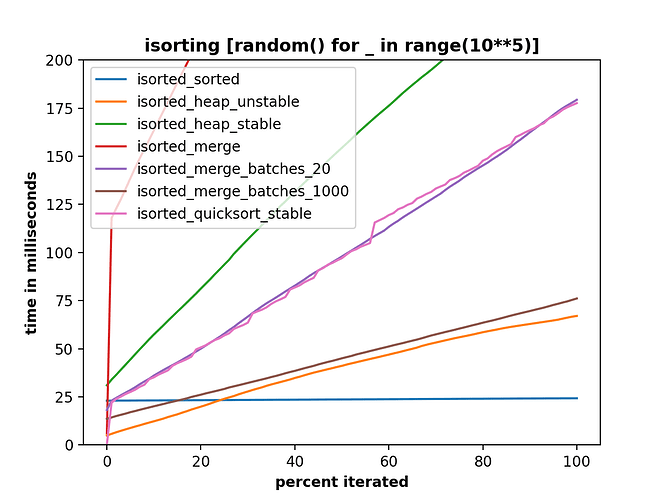
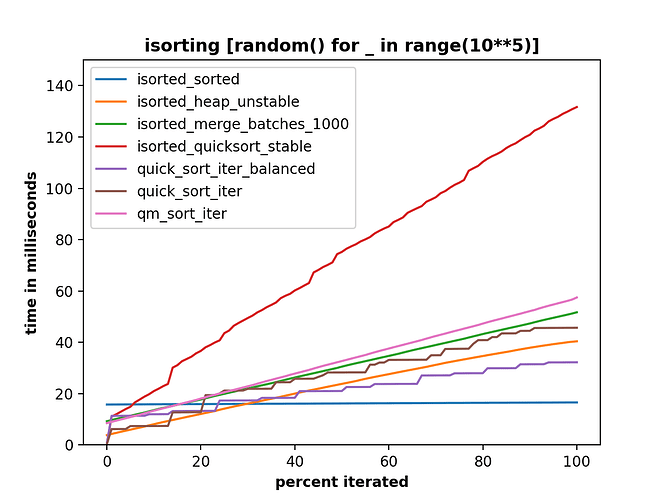
quick_sort_iter_balanced: Modified quicksortquick_sort_iter Modified quicksort as above, but skewed towards lower initialisation at the cost of total runtimeqm_sort_iter - batched 1000 run merged with merge functions from precious challengeSo to me it seems that it is indeed possible to implement pure python iterator recipe that is performant and sensible for random data.
But I am having troubles to incorporate any sort of pattern beating behaviour without loosing a lot of performance.
times = {
'isorted_sorted': [15.77, 15.78, 15.79, 15.8, 15.81, 15.82, 15.82, 15.83, 15.84, 15.85, 15.86, 15.87, 15.88, 15.88, 15.89, 15.9, 15.91, 15.92, 15.93, 15.93, 15.94, 15.95, 15.96, 15.97, 15.97, 15.98, 15.99, 16.0, 16.01, 16.02, 16.03, 16.03, 16.04, 16.05, 16.06, 16.07, 16.08, 16.08, 16.09, 16.1, 16.11, 16.12, 16.12, 16.13, 16.14, 16.15, 16.16, 16.17, 16.17, 16.18, 16.19, 16.2, 16.21, 16.22, 16.22, 16.23, 16.24, 16.25, 16.26, 16.26, 16.27, 16.28, 16.29, 16.3, 16.3, 16.31, 16.32, 16.33, 16.34, 16.34, 16.35, 16.36, 16.37, 16.38, 16.38, 16.39, 16.4, 16.41, 16.42, 16.43, 16.43, 16.44, 16.45, 16.46, 16.47, 16.47, 16.48, 16.49, 16.5, 16.5, 16.51, 16.52, 16.53, 16.54, 16.54, 16.55, 16.56, 16.57, 16.58, 16.58, 16.59],
'isorted_heap_unstable': [3.83, 4.3, 4.73, 5.15, 5.57, 5.97, 6.38, 6.78, 7.19, 7.66, 8.09, 8.53, 8.94, 9.34, 9.74, 10.13, 10.53, 10.92, 11.31, 11.7, 12.09, 12.48, 12.87, 13.25, 13.73, 14.16, 14.58, 14.97, 15.36, 15.74, 16.12, 16.5, 16.88, 17.26, 17.65, 18.03, 18.4, 18.78, 19.21, 19.62, 20.03, 20.44, 20.82, 21.2, 21.57, 21.95, 22.32, 22.7, 23.07, 23.44, 23.81, 24.18, 24.55, 24.92, 25.36, 25.77, 26.16, 26.53, 26.89, 27.25, 27.61, 27.97, 28.33, 28.69, 29.04, 29.39, 29.74, 30.09, 30.44, 30.84, 31.22, 31.59, 32.0, 32.34, 32.68, 33.02, 33.35, 33.68, 34.01, 34.34, 34.66, 34.99, 35.31, 35.62, 35.94, 36.24, 36.57, 36.93, 37.26, 37.58, 37.89, 38.18, 38.47, 38.75, 39.02, 39.28, 39.53, 39.76, 40.03, 40.23, 40.4],
# 'isorted_heap_stable': [18.02, 19.24, 20.47, 21.72, 22.89, 24.17, 25.58, 27.2, 28.78, 30.34, 31.9, 33.56, 35.12, 36.65, 38.25, 39.8, 41.32, 42.83, 44.45, 45.99, 47.51, 49.0, 50.6, 52.09, 53.58, 55.08, 56.65, 58.13, 59.58, 61.12, 62.63, 64.1, 65.56, 67.08, 68.56, 70.0, 71.43, 72.93, 74.4, 75.83, 77.25, 78.81, 80.35, 81.87, 83.37, 84.91, 86.42, 87.92, 89.41, 90.91, 92.37, 93.81, 95.26, 96.74, 98.17, 99.59, 100.99, 102.41, 103.8, 105.16, 106.52, 107.9, 109.27, 110.6, 111.94, 113.27, 114.6, 115.89, 117.17, 118.49, 119.81, 121.08, 122.38, 123.62, 124.86, 126.1, 127.3, 128.5, 129.67, 130.86, 132.03, 133.15, 134.26, 135.35, 136.42, 137.52, 138.55, 139.56, 140.53, 141.46, 142.44, 143.39, 144.27, 145.1, 145.89, 146.66, 147.4, 148.16, 148.91, 149.55, 150.07],
# 'isorted_merge': [6.04, 128.75, 130.97, 133.22, 135.45, 138.38, 141.47, 144.45, 147.48, 150.67, 153.82, 157.31, 160.82, 164.41, 167.98, 171.55, 175.13, 178.67, 182.26, 186.29, 189.98, 194.03, 198.47, 202.77, 206.72, 210.51, 214.27, 217.89, 221.62, 225.18, 228.72, 232.14, 235.39, 238.7, 241.89, 245.16, 248.28, 251.53, 254.87, 258.05, 261.22, 264.41, 267.61, 270.72, 273.95, 277.05, 280.2, 283.26, 286.42, 290.37, 293.86, 297.3, 300.29, 303.2, 306.19, 308.93, 311.67, 314.57, 317.15, 319.73, 322.54, 325.24, 327.74, 330.38, 332.84, 335.23, 337.72, 340.3, 342.7, 344.93, 347.39, 349.67, 351.89, 354.2, 356.62, 358.88, 361.21, 363.76, 366.05, 368.15, 370.24, 372.48, 374.47, 376.34, 378.38, 380.64, 382.7, 384.72, 386.67, 388.84, 390.85, 392.72, 394.63, 396.52, 398.25, 399.87, 401.41, 402.81, 404.2, 405.69, 406.89],
# 'isorted_merge_batches_20': [11.35, 15.65, 16.54, 17.41, 18.43, 19.33, 20.21, 21.09, 21.96, 22.83, 23.79, 24.72, 25.59, 26.45, 27.31, 28.18, 29.05, 30.02, 30.91, 31.77, 32.64, 33.51, 34.36, 35.31, 36.23, 37.1, 37.96, 38.82, 39.69, 40.56, 41.53, 42.42, 43.29, 44.15, 45.01, 45.88, 46.81, 47.77, 48.65, 49.61, 50.5, 51.39, 52.26, 53.27, 54.18, 55.08, 55.97, 56.86, 57.75, 58.74, 59.68, 60.58, 61.48, 62.38, 63.27, 64.25, 65.21, 66.11, 67.01, 67.9, 68.81, 69.73, 70.74, 71.65, 72.55, 73.46, 74.36, 75.27, 76.27, 77.2, 78.09, 78.98, 79.92, 80.83, 81.81, 82.78, 83.75, 84.71, 85.66, 86.6, 87.57, 88.54, 89.48, 90.43, 91.37, 92.31, 93.26, 94.24, 95.18, 96.12, 97.05, 97.99, 98.95, 99.95, 100.89, 101.82, 102.76, 103.69, 104.66, 105.67, 106.59],
'isorted_merge_batches_1000': [9.25, 9.74, 10.16, 10.57, 10.98, 11.39, 11.8, 12.22, 12.63, 13.12, 13.58, 14.03, 14.44, 14.85, 15.26, 15.68, 16.09, 16.5, 16.91, 17.33, 17.74, 18.23, 18.68, 19.12, 19.54, 19.95, 20.36, 20.77, 21.19, 21.6, 22.01, 22.42, 22.84, 23.25, 23.66, 24.07, 24.49, 24.97, 25.43, 25.87, 26.3, 26.72, 27.14, 27.55, 27.96, 28.37, 28.79, 29.2, 29.62, 30.03, 30.53, 30.98, 31.42, 31.83, 32.24, 32.65, 33.06, 33.47, 33.9, 34.3, 34.71, 35.12, 35.53, 36.0, 36.45, 36.9, 37.32, 37.73, 38.14, 38.54, 38.96, 39.37, 39.78, 40.19, 40.6, 41.0, 41.41, 41.88, 42.33, 42.77, 43.24, 43.65, 44.06, 44.47, 44.88, 45.29, 45.7, 46.1, 46.51, 46.92, 47.34, 47.82, 48.28, 48.73, 49.14, 49.55, 49.96, 50.38, 50.79, 51.22, 51.71],
'isorted_quicksort_stable': [0.21, 11.11, 11.96, 12.99, 14.0, 14.89, 16.63, 17.73, 18.85, 19.8, 21.0, 21.92, 22.94, 23.8, 30.13, 31.1, 32.65, 33.53, 34.42, 35.73, 36.67, 38.07, 38.94, 39.96, 40.77, 43.58, 44.58, 46.44, 47.52, 48.5, 49.49, 50.42, 51.65, 52.56, 53.68, 54.57, 55.53, 57.2, 58.15, 58.91, 60.22, 61.12, 62.13, 63.09, 67.24, 68.19, 69.32, 70.17, 71.14, 74.37, 75.22, 76.48, 77.39, 78.21, 79.32, 80.11, 81.02, 82.44, 83.45, 84.35, 85.13, 86.85, 87.71, 88.65, 90.47, 91.38, 92.25, 93.07, 94.79, 95.63, 96.53, 98.08, 98.93, 100.23, 101.35, 102.21, 103.25, 106.85, 107.83, 108.75, 110.31, 111.54, 112.54, 113.36, 114.35, 115.69, 116.74, 117.55, 118.79, 119.94, 120.86, 122.49, 123.33, 124.35, 126.06, 127.04, 127.87, 129.01, 129.87, 130.83, 131.68],
'quick_sort_iter_balanced': [0.67, 11.35, 11.36, 11.36, 11.37, 11.38, 11.39, 11.4, 11.4, 11.98, 11.99, 12.0, 12.01, 12.02, 13.22, 13.23, 13.24, 13.25, 13.26, 13.27, 13.28, 13.29, 13.3, 13.31, 17.31, 17.32, 17.33, 17.34, 17.35, 17.35, 17.36, 17.37, 17.38, 18.35, 18.36, 18.36, 18.37, 18.38, 18.39, 18.4, 18.4, 20.96, 20.97, 20.98, 20.99, 21.0, 21.01, 21.01, 21.02, 21.03, 21.04, 22.58, 22.59, 22.6, 22.6, 22.61, 22.62, 23.75, 23.76, 23.76, 23.77, 23.78, 23.79, 23.8, 23.8, 23.81, 23.82, 27.09, 27.1, 27.11, 27.12, 27.13, 27.14, 27.14, 27.94, 27.94, 27.95, 27.96, 27.97, 27.98, 27.98, 29.89, 29.9, 29.91, 29.92, 29.92, 29.93, 29.94, 31.44, 31.45, 31.46, 31.46, 31.47, 31.48, 32.18, 32.19, 32.19, 32.2, 32.21, 32.22, 32.23],
# 'quick_sort_iter_balanced_cy': [0.72, 5.87, 5.88, 5.89, 5.9, 5.91, 5.92, 7.02, 7.03, 7.04, 7.05, 7.05, 7.06, 7.07, 7.08, 7.09, 8.0, 8.01, 8.02, 8.03, 9.15, 9.16, 9.17, 9.18, 9.19, 10.04, 10.05, 10.05, 10.06, 10.07, 10.08, 10.09, 10.09, 14.14, 14.15, 14.16, 14.17, 14.18, 14.19, 14.2, 15.45, 15.45, 15.46, 15.47, 15.48, 15.49, 15.49, 15.5, 15.51, 15.52, 16.65, 16.66, 16.67, 16.68, 16.69, 16.69, 16.7, 17.2, 17.21, 17.22, 17.23, 17.24, 20.2, 20.21, 20.22, 20.23, 20.24, 20.24, 20.25, 20.66, 20.67, 20.68, 20.69, 21.2, 21.21, 21.21, 21.22, 21.58, 21.59, 21.6, 23.38, 23.39, 23.4, 23.41, 23.41, 23.42, 23.43, 23.44, 24.87, 24.88, 24.89, 24.9, 24.91, 24.91, 24.92, 24.93, 24.94, 24.95, 25.24, 25.25, 25.26],
'quick_sort_iter': [0.34, 6.2, 6.21, 6.22, 6.22, 7.36, 7.37, 7.37, 7.38, 7.39, 7.4, 7.41, 7.42, 7.43, 12.7, 12.72, 12.74, 12.76, 12.77, 12.79, 12.81, 19.42, 19.43, 19.44, 20.12, 21.2, 21.2, 21.21, 21.22, 21.23, 21.89, 21.9, 21.91, 21.91, 21.92, 21.93, 24.43, 24.44, 24.45, 24.46, 25.81, 25.81, 25.82, 25.83, 25.84, 26.52, 27.18, 28.25, 28.26, 28.26, 28.27, 28.28, 28.29, 28.3, 28.3, 28.31, 31.29, 31.3, 32.11, 32.12, 33.16, 33.17, 33.18, 33.19, 33.19, 33.2, 33.21, 33.22, 33.23, 34.95, 34.96, 34.97, 37.41, 37.43, 37.46, 37.48, 37.5, 37.53, 39.47, 40.84, 40.85, 40.86, 42.04, 42.05, 43.47, 43.48, 43.49, 43.5, 44.46, 44.47, 44.48, 45.58, 45.59, 45.6, 45.61, 45.62, 45.63, 45.64, 45.65, 45.66, 45.67],
# 'quick_sort_iter_cy': [0.38, 4.17, 4.18, 4.19, 4.2, 5.22, 5.23, 5.24, 5.25, 5.26, 5.26, 5.27, 5.28, 5.29, 8.69, 8.7, 8.7, 8.71, 8.72, 8.73, 8.74, 12.66, 12.67, 12.67, 13.15, 14.06, 14.07, 14.08, 14.08, 14.09, 14.77, 14.78, 14.79, 14.79, 14.8, 14.81, 16.68, 16.69, 16.7, 16.71, 17.68, 17.69, 17.7, 17.71, 17.72, 18.19, 18.76, 19.98, 19.99, 20.0, 20.01, 20.02, 20.03, 20.04, 20.05, 20.06, 21.96, 21.97, 22.59, 22.6, 23.68, 23.69, 23.7, 23.71, 23.72, 23.73, 23.74, 23.74, 23.75, 25.15, 25.16, 25.17, 26.74, 26.75, 26.76, 26.76, 26.77, 26.78, 27.53, 28.49, 28.5, 28.5, 29.17, 29.18, 30.15, 30.18, 30.19, 30.2, 31.02, 31.03, 31.04, 32.16, 32.17, 32.17, 32.18, 32.19, 32.2, 32.22, 32.23, 32.25, 32.25],
'qm_sort_iter': [8.51, 9.02, 9.48, 9.95, 10.41, 10.88, 11.34, 11.81, 12.35, 12.87, 13.37, 13.83, 14.3, 14.76, 15.23, 15.7, 16.16, 16.62, 17.09, 17.55, 18.09, 18.6, 19.11, 19.58, 20.07, 20.54, 21.0, 21.47, 21.94, 22.41, 22.87, 23.34, 23.88, 24.4, 24.91, 25.38, 25.86, 26.33, 26.8, 27.35, 27.82, 28.3, 28.77, 29.24, 29.79, 30.31, 30.82, 31.29, 31.76, 32.23, 32.7, 33.18, 33.65, 34.12, 34.59, 35.06, 35.61, 36.14, 36.64, 37.11, 37.59, 38.07, 38.54, 39.01, 39.48, 39.96, 40.43, 40.9, 41.45, 41.97, 42.47, 42.94, 43.41, 43.91, 44.39, 44.86, 45.33, 45.8, 46.27, 46.75, 47.31, 47.83, 48.33, 48.8, 49.27, 49.75, 50.22, 50.69, 51.16, 51.67, 52.15, 52.62, 53.21, 53.74, 54.25, 54.72, 55.2, 55.67, 56.15, 56.67, 57.48],
# 'qm_sort_iter_cy': [8.54, 8.84, 9.1, 9.36, 9.68, 9.97, 10.26, 10.54, 10.82, 11.09, 11.34, 11.61, 11.86, 12.13, 12.39, 12.65, 12.9, 13.16, 13.42, 13.68, 13.94, 14.2, 14.45, 14.72, 14.97, 15.29, 15.57, 15.86, 16.14, 16.43, 16.68, 16.94, 17.2, 17.46, 17.72, 17.98, 18.24, 18.54, 18.8, 19.05, 19.31, 19.56, 19.82, 20.08, 20.34, 20.59, 20.85, 21.14, 21.43, 21.71, 21.99, 22.28, 22.53, 22.79, 23.05, 23.31, 23.56, 23.82, 24.08, 24.33, 24.59, 24.85, 25.11, 25.36, 25.62, 25.88, 26.13, 26.39, 26.65, 26.97, 27.25, 27.54, 27.82, 28.1, 28.35, 28.61, 28.86, 29.12, 29.37, 29.63, 29.92, 30.19, 30.46, 30.73, 30.99, 31.26, 31.53, 31.8, 32.07, 32.38, 32.67, 32.97, 33.27, 33.58, 33.88, 34.16, 34.44, 34.73, 35.02, 35.31, 36.11]
}
My bucketed merge is the same as yours, just a bit worse.
My quick_sort_iter code:
import random
import itertools as itl
import operator as opr
_QSEMPTY = object()
def quick_sort_iter(arr, p=1, mn_nfb=1000):
assert 1 <= p <= 9
if not isinstance(arr, (list, tuple)):
arr = list(arr)
n = len(arr)
nfb = max(mn_nfb, n // 10)
if n <= nfb:
if type(arr) is list:
arr.sort()
return iter(arr)
else:
return iter(sorted(arr))
q = [(False, arr, n)]
del arr
its = _qs_inner(q, p, nfb)
return itl.chain.from_iterable(its)
def _qs_inner(q, p, nfb):
qappend = q.append
pop = q.pop
rns = None
while q:
is_sorted, arr, n = pop()
if arr:
if is_sorted:
yield arr
elif n <= nfb:
arr.sort()
yield arr
else:
if rns is None:
rns = _qs_get_rns(11)
pivot = _qs_get_pivot_points(arr, rns, n)[p]
lt, eq, gt, lt_dir, gt_dir = _qs_partition(arr, pivot)
if lt_dir == -1:
lt = reversed(lt)
lt_dir = 1
if gt_dir == -1:
gt = reversed(gt)
gt_dir = 1
if gt_dir == 1:
qappend((True, gt, None))
else:
qappend((False, gt, len(gt)))
qappend((True, eq, None))
if lt_dir == 1:
qappend((True, lt, None))
else:
qappend((False, lt, len(lt)))
def _qs_partition(arr, pivot):
lt, eq, gt = [], [], []
lappend = lt.append
eappend = eq.append
gappend = gt.append
x_lt = x_gt = _QSEMPTY
lt_dir = -2 # -2: uninitialised 0: jitter
gt_dir = -2 # 1: increasing, -1: decreasing
for x in arr:
if x < pivot:
if lt_dir:
if x_lt is _QSEMPTY:
x_lt = x
elif lt_dir == -2:
if x >= x_lt:
lt_dir = 1
else:
lt_dir = -1
x_lt = x
elif lt_dir == 1:
if x >= x_lt:
x_lt = x
else:
lt_dir = 0
else: # lt_dir == -1
if x < x_lt:
x_lt = x
else:
lt_dir = 0
lappend(x)
elif x > pivot:
if gt_dir:
if x_gt is _QSEMPTY:
x_gt = x
elif gt_dir == -2:
if x >= x_gt:
gt_dir = 1
else:
gt_dir = -1
x_gt = x
elif gt_dir == 1:
if x >= x_gt:
x_gt = x
else:
gt_dir = 0
else: # gt_dir == -1
if x < x_gt:
x_gt = x
else:
gt_dir = 0
gappend(x)
elif x is pivot or x == pivot:
eappend(x)
else:
raise ValueError('Malicious Data to sort')
if not eq:
raise ValueError('Malicious Data to sort')
return lt, eq, gt, lt_dir, gt_dir
def _qs_get_rns(n, seed=None):
assert n > 2
if seed is not None:
random.seed(seed)
rns = {0, 999}
add = rns.add
while len(rns) < n:
rn = int(random.random() * 1000)
if rn != 1000:
add(rn)
return list(rns)
def _qs_get_pivot_points(arr, rns, n):
return sorted([arr[n * rn // 1000] for rn in rns])