Define an additive version of Euler's totient function

Python Help
1

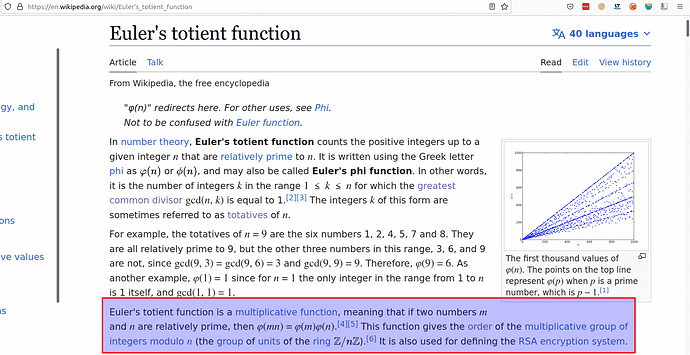
The ordinary Euler’s totient is a multiplicative function, as represented below:

image
image1584×815 189 KB

I want to revise this function into a new additive version as described below:

  1. If p is a prime, then
    phi( p ^ k ) := p ^ k - p ^ (k -1) = p ^ k ( 1- 1/p)

  2. If m and m’ are relatively prime then
    phi( m * m’) := phi(m) + phi(m’)

unless m = 2 and n is odd, in which case
phi(2n) := phi(n)

I want to create this function in python and then compute its possible function values for a given positive integer, for example, phi(6), phi(25), phi(50) and so on.

Any tips for achieving this goal will be appreciated.

Regards,
Zhao