And hello reduce(lambda a, c: digits.index(c) + sum(map(int, digits)) * int(a), f"{len(digits) >> True:b}"). 
2 Likes
A very clever way of spelling 45**2 + 1. Nice! 
2 Likes
Given dominoes \begin{bmatrix}1\\11\end{bmatrix}, \begin{bmatrix}1110\\010\end{bmatrix} and \begin{bmatrix}1010\\10\end{bmatrix}, concatenate copies of them such that the word at the top equals the word at the bottom.[1]
4 Likes
Solving that dominoes puzzle (I first solved it by hand, but then was curious whether there are alternative solutions (other than just repeating the one) and was too lazy to think, plus it was another opportunity to advocate the use of parallel combinatoric iterators instead of using just one with more complicated processing of its results.)
from itertools import product
for n in range(1, 10):
for a, b in zip(
map(''.join, product(('1', '1110', '1010'), repeat=n)),
map(''.join, product(('11', '010', '10'), repeat=n))
):
if a == b:
print(int(a, 2))
2 Likes
If you want something based on an integral that looks a bit more inscrutable:
\frac{1}{12}\sum_{k=1}^{4}\left(10^{4-k}\int_0^k -20x^3+138x^2-254x+110\,dx\right)
3 Likes
If these puzzles are too obscure for you, you’re not alone 
Try this one making the rounds on Faceook:
- Write down the year you were born.
- Add the age you’ll be at the end of this year.
- What do you get?
Surprise! It’s amazing how many people are baffled by this. I try to help by assuring them it only happens once per 737 years (which is 11 * 67, just adding to the mystery)
3 Likes
Apart the constants, integral of the \frac{1}{1+x^2} term is arctan(x).
(+C of course)
So do the rest of the math :))
3 Likes
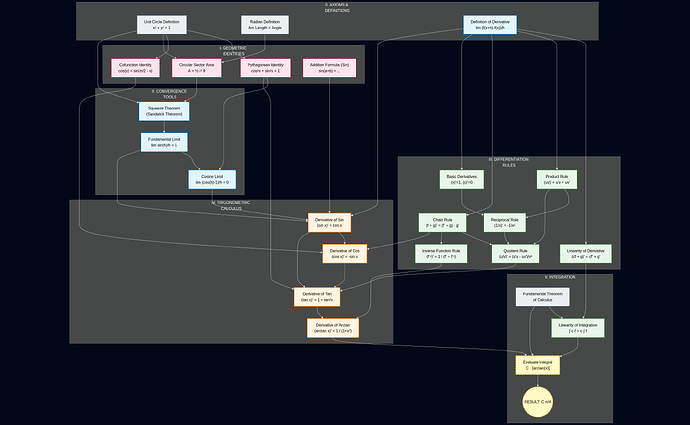
One of my favorite use of AI tools is to generate mermaid dependency graphs for math results, and in that case it nicely applies to the 1/(1+x²) integral:
Feel free to edit it here
For each box there exists a concise proof, and the edges gives a good hint on where to start.
That’s a fun exercise if like me you forgot how most of those results are meant to be proved
2 Likes
And always remember that the AI is a charlatan that knows a lot of words, but it is still a charlatan. I don’t know what that arrow from the Fundamental Theorem of Calculus to Linearity of integration is doing, or the one from Unit Circle Definition to Cofunction Identity. Who knows how many more things are wrong in there. It is probably not worth anyone’s time to check.
2 Likes
I understand your suspicions about AI, I actually had to iterate for quite a bit until I got a result I was happy with. I did check most of those links, but I might have missed a couple of mistakes here and there. Also there are many ways to make a dependency graph, and I did make some choices about proofs that were more pleasing to me, so there’s a bit subjectivity involved.
Well, since this theorem links the concept of differentiating with the concept of integrating I thought it makes sense here to show that the linearity of differentiation leads to the linearity of integration. But maybe it should go in the “axioms and definitions” section, since it is a fundamental result.
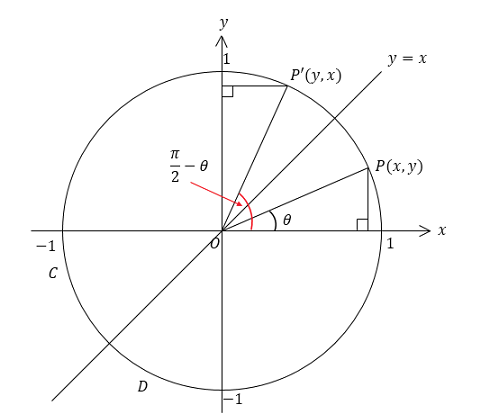
I’m fine with this part too: the cofunction identity here can be geometrically illustrated by taking the unit circle and flipping it over the y = x line. This way, cos becomes sin and sin becomes cos for the new angle going from the top of the unit circle to the projected point.
1 Like
I’m really rusty… I remembered the trick with this kind of integrals is the substitution with some trigonometric function, but too rusty, too tired and too late… so I asked for an hint to Socrates:
* When I ask you to be Socrates, you should not answer directly to my questions. Instead, you should ask me a single question. When I answer your question, you should ask me another single question, without saying to me if you think my answer was right or not. The process can change your initial beliefs, and I can also ask you a question instead of answering your question. Anyway, you must not tell me anything, but only ask as usual another question. This will end when we both arrive to a conclusion, free from contradictions, that satisfies us both -- e.g. no one has anything more to ask or to point out. This will be our shared Truth.
Now I’m going to drink a shot of vodka for every time I wrote “question.”
Uuuufffff… it’s too late and I’m tired. Anyway:
spoiler
I’m quite sure the pest is February. Right?
…wait a moment. Only years are mentioned. So it’s normal that the result is the current year, 2026, isn’t it?
1 Like
Exactly, it’s normal. To break this, someone needs to travel so close to light speed they lose a year due to time dilation via the Twins Pardox. Or cryosleep needs to be invented, and society needs to change how a person’s age is legally defined.
2 Likes
Imagine if, whenever you drink a legally-recognized Potion of Youth, your date of birth moves one year into the future.
And if you then drink more of them than your age in years…
Then your legal date of birth would be in the future. I don’t recommend it, though; you can’t vote or drink until you have a legal age of positive 18, although on the plus side, you can probably get into theatres and amusement parks for free with an accompanying adult.
1 Like
It exists. Is it not the year 3k?
2 Likes
Absolutely. That the year you were born plus the age you’ll be at the end of the year is the current year is always true. It’s a trivial consequence of how “the age you’ll be” is defined.
Much more subtly, the Gregorian calendar repeats with a period of exactly 400 years, so any calendar-based claim of “happens only once every N years” must be bogus unless N divides 400.
2 Likes
But it’s fun to claim that this particular year is special. People like weird factoids like that if they think they’re rare.
2 Likes
>>> from sympy import *
>>> x=sympy.symbols('x')
>>> sympy.integrate(8104/(pi*(1+x**2)), (x, 0,1))
2026
4 Likes