Karatsuba is a large amount of code compared to grade school multiplication. Every line is another potential source of errors, and an eternal maintenance burden. You’ll write your fancy new code once and then go away, leaving it to others to clean up problems forever after  .
.
Compiling packages is just business as usual for Linux-heads. On Windows there are compiled GMP libraries ready to download.
Who is the real target audience? Popular Python packages like mpmath already exploit GMP if it’s installed. People who need very large integers typically need many different kinds of operations on them to “run really fast”. It doesn’t end with multiplication.
Arbitrary precision floats are one thing decimal supports, but that includes arbitrary precision integers (although you need to set the maximum precision in advance). Indeed, when bigint input and/or output eed to be in base 10, decimal can be the way to go for integer arithmetic - CPython’s power-of-2 to/from power-of-10 I/O base conversion algorithms take quadratic time. In decimal, base-10 I/O is close to “free”.
For example, here I cut a user’s runtime from hours to under a minute just by switching to use decimal.
Using a larger base for CPython’s internal “digits” holds more attraction to me, but is also fraught with potential problems. As is, we rely on that a double-width digit product can be obtained in portable plain old C, and held in a native platform C type with at least one bit to spare (and while memory of details has faded, I seem to recall there’s at least one place in the code that relies on that there are at least two bits to spare),. CPython gets ported to a lot of platforms, and the amount of time porters to brand new platforms have had to spend getting Python’s bigints “to work” is approximately 0 seconds.
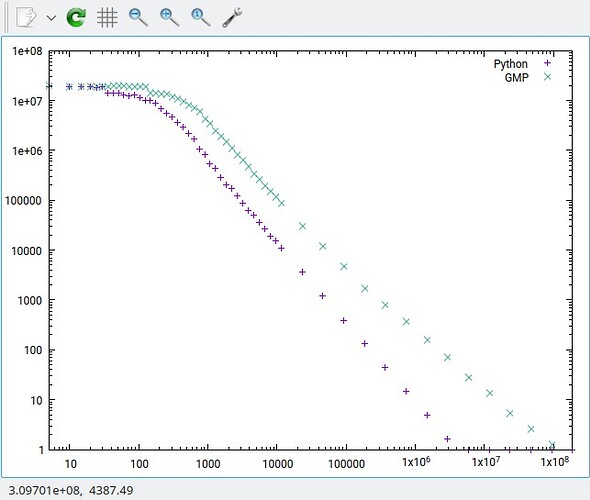
GMP is eager to use 64-bit “limbs” (digits) on modern boxes, but they also don’t hesitate to dip into assembler to get at the HW instructions that make doing so practical. C is a poor language for this purpose.
But that’s enough from me. In short, my position is that people who really need fast bigint arithmetic are - and always will be - better off using GMP, which is already available, while bigints are “fast enough” already in CPython for casual bigint users. If we had a dozen numeric experts regularly contributing who were keen to add & maintain fancier stuff, fine - but we don’t. In the old days I fixed every numeric problem that showed up, but now it’s much more Mark Dickinson.
Simple changes are welcome, but more than that requires weighing the likely tiny benefit for most users against the likelihood that the original author won’t maintain their work. Karatsuba relies only on very simple algebra, but the more-advanced methods require background most programmers just don’t have. The heavy lifting in decimal is done by libmpdec, an external project maintained by Stefan Krah.
 .
.