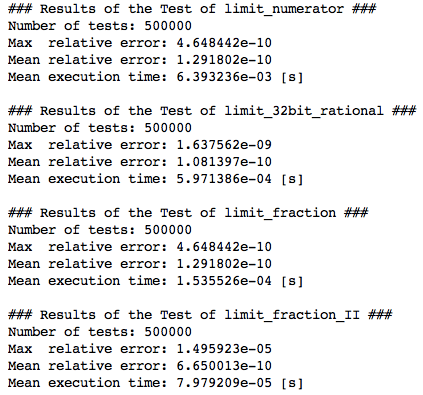
Hi Dominik,
What is wrong is that the Discuss software does not email images, it
emails an internal markdown code that is unviewable.
But why are you taking screenshots of text? Screenshots of GUI
applications makes sense: if you want to show a problem with a GUI, you
need to see the graphical elements. But your results are text.
Not everyone can see screenshots at all. I know that there is at least
one highly respected core Python developer whose eyesight has
deteriated to the point that he is (I think) legally blind. I’ve worked
with no fewer than three developers who are likewise are legally blind,
all had extreme problems dealing with screenshots. I know at least one
person who is completely blind and uses a screen reader to read emails.
I never realised that he was blind until he apologised in advance for
not being able to understand something I had written because his screen
reader was mispronouncing the words and he couldn’t tell what they were.
Screen shots of text discriminate against the visually impaired and
blind. They are also inconvenient and annoying for many fully sighted
readers too.
I said:
"I would expect that your timing code is measuring almost nothing but
noise."
and you disagreed:
“It seems that your expectation is wrong.”
What makes you say that?
I asked what you were hoping to demonstrate with the cumulative errors,
and you responded by saying:
"The cumulative error is divided by the number of test runs at the
end, please have a look at the __ str __ method."
Yes, I know that. But I still don’t know why you are calculating those
errors in the first place. What do you think the errors show?
Are you trying to find the algorithm with the smallest error? The
smallest error is the identity function that just returns the number
unchanged. Walk me through your logic as if I were five please.
You said:
“”"
I am calculating the differences between the result of each
limit*-function and the random FLOAT it has been fed with:
see “abs(float(fraction) - randomValueF) / abs(randomValueF)”
“”"
Yes, I know that. Every float is equal to an exact fraction.
(To be pedantic: only the finite floats. NANs and INFs excepted.)
For example, the float math.pi is exactly equal to the fraction
884279719003555/281474976710656.
If we reduce that fraction to have a smaller denominator, we are
naturally going to introduce some difference. The fraction 22/7 is the
closest fraction to math.pi with the denominator less than 10.
The difference between math.pi and 22/7 is 0.0012644892673497412.
(I know that you are calculating the relative error, not the absolute
error. You are dividing by the original number. But that doesn’t change
my point, so for simplicity I am going to continue with absolute error.)
The difference between math.pi and 311/99 is even smaller, just
0.00017851217565170184, so that’s better, right?
Not if we want to limit the denominator to be less than ten! 99 is not
less than ten.
In your case, you have an additional constraint: you also want to limit
the numerator, not just the denominator. But the principle applies: we
are not just trying to find the smallest difference between the original
number and the new number. For that, we could just use the original
number unchanged.
So the bottom line here, if we have four different algorithms for
limiting the numerator and denominator of a fraction, they must
return the same (numerator, denominator) pair. If they don’t, some of
them are simply wrong and returning the wrong result.
To be clear:
If any two algorithms return a different (num, den) pair, then
at least one of them is wrong. They might both be wrong, but they
can’t both be right. Only one num/den fraction can be the closest to the
original number.
If all four return the same pair, that’s reasonable evidence that they
are probably correct. It is unlikely that four independent algorithms
would all just happen to return the same wrong answer. (Very unlikely,
but not impossible.) If any one of them is different, that’s a good sign
that it is the wrong answer.
But if all four are different, that shows that at least three of them
are wrong, maybe all four are wrong. It’s not a matter of pulling out
the one which is least wrong on average and calling it the best.
Looking at the error terms and picking the function with the smallest
error terms is the wrong way to analyse this. You are measuring the
wrong thing.
You suggested that you are trying to:
"COMPARE the (mean) performance of the four algorithm versions (so, your
“noise” should cancel out sufficiently, right?)."
I’m afraid not. Errors only cancels out when they are equally likely to
be positive or negative. If I have a piece of wood exactly 78.3 cm long,
and ask six people to measure it, they are likely to get results
something like this:
77.9, 78.0, 78.2, 78.5, 78.5, 78.7
and the errors cancel out. (In this case, they cancel out exactly,
because I made the numbers up. In the real world, we are rarely that
lucky.)
But noise when timing code is not like that. The errors are always
one-sided: your measured time will never have a negative error.
Suppose the “true” time it takes your CPU to compute a result is, let’s
say, exactly 10µs. Then your timing code will probably
measure something like:
12, 15, 16, 18, 19, 26 µs
and the best estimate of the true time to run the code is the minimum,
12µs, not the mean, 17.7µs.
Noise does not cancel out because it always adds time to the
measurement, it never subtracts it. Taking the average just averages the
noise. It gets you no closer to the actual execution cost of the code,
it just moves you further away.
Worse, if the code snippet is small and fast enough, the noise might
completely overwhelm the measurement. If your results are 12µs etc
above, we have no way of knowing that the true computational cost is
actually 10µs. It might be 1µs, and the rest of the measurement is all
noise.
This is why we have the timeit module. The timeit module is designed to
measure the running cost of small code snippets, with as little noise
as possible.
It cannot eliminate all noise – nothing can. But it can try to make it
as small as possible, within the Python interpreter at least. It can’t
do anything about noise from the OS, e.g. other processes running.
Regarding the use of eval on the function names, passed as strings, no,
I did not overlook the use of self.testFctNames to print the names of
the functions. Although you might have overlooked that functions know
their own names and you can print those 
>>> def func(): pass
...
>>> func.__name__
'func'
Inside a Python script, there is little need to pass function names
separately from the function themselves. The only exception I can think
of is if you are getting the names from user-provided data, e.g. read
from a file, or a command line, or a GUI input widget (say, for a
calculator app). You can only get user input as strings.
Even there, especially there, you should not use eval to evaluate the
string to get the function. Using eval on untrusted user input is
very dangerous. Instead, use a global lookup:
func = globals()[name]
But in your case, you don’t need that since you can just pass the
function object and retrieve the name from the function, not the
function from the name.