I did some benchmarking stuff on the fastest way to find an item in a list. I have found that converting a list into an iterator and then checking if exists in that iterator is relatively fast. However, at some point, it starts to go crazy.
Now, I am wondering the reason why the iter function behaves that way on relatively large lists.
I don’t understand how you got your results. The performance of in with iterators and lists should behave similarly: the speed will depend on the number of items, or in Big Oh notation, both are O(N).
There may be small differences due to the overhead of converting the list into an iterator, or differences between the list __contains__ dunder and the interpreters generic fall-back code for containment checks in an iterator. And I would expect lists to be faster – if they are not, that is an opportunity to speed them up.
A list can perform its own internal check, by testing each element in the internal array at full C speed. That is fast, but will depend on the number of items in the list: on average, the list has to check half the items for a successful result, and all of the items for an unsuccessful result. So that’s O(N).
Iterators cannot have a dedicated dunder, so they have to fall back on generic iteration:
for element in iterator:
if element == needle: return True
return False
although the interpreter can do this at C speed, there is still the iterator overhead compared to lists. Plus the overhead of creating the iterator object itself. So I expect that lists and iterators should behave with the same O(N) performance, with perhaps lists a tiny bit faster.
I will run my own tests shortly to see what I find.
I ran some benchmarks, and I can find no evidence of a massive performance drop for iterators around ten million items. (Nor would I expect to.)
Here are the numbers from my PC:
# Obj Size Time Obj Size Time
1. list 10 1.098e-07 | iter 10 1.796e-07 |
2. list 20 1.974e-07 | iter 20 2.768e-07 |
3. list 40 3.668e-07 | iter 40 4.66e-07 |
4. list 80 7.075e-07 | iter 80 8.383e-07 |
5. list 160 1.416e-06 | iter 160 1.631e-06 |
6. list 320 2.841e-06 | iter 320 3.22e-06 |
7. list 640 5.712e-06 | iter 640 6.49e-06 |
8. list 1280 1.179e-05 | iter 1280 1.321e-05 |
9. list 2560 2.424e-05 | iter 2560 2.681e-05 |
10. list 5120 4.866e-05 | iter 5120 5.41e-05 |
11. list 10240 9.768e-05 | iter 10240 0.0001067 |
12. list 20480 0.0001908 | iter 20480 0.0002139 |
13. list 40960 0.0003896 | iter 40960 0.0004359 |
14. list 81920 0.0008147 | iter 81920 0.0009132 |
15. list 163840 0.001693 | iter 163840 0.001904 |
16. list 327680 0.003436 | iter 327680 0.003844 |
17. list 655360 0.006941 | iter 655360 0.007768 |
18. list 1310720 0.01395 | iter 1310720 0.01556 |
19. list 2621440 0.0279 | iter 2621440 0.03267 |
20. list 5242880 0.05779 | iter 5242880 0.06501 |
21. list 10485760 0.118 | iter 10485760 0.1329 |
22. list 20971520 0.2411 | iter 20971520 0.2714 |
Total elapsed time: 300.235714 seconds
As expected, lists and iterators show the same O(N) behaviour. Doubling the number of items roughly doubles the time taken. Searching lists is consistently slightly faster than searching an iterator.
Here is my benchmark code:
# Benchmark ``in`` operator for lists and iterators.
from timeit import Timer
from time import time
# Testing unsuccessful searches only.
list_snippet = "-999 in mylist"
iter_snippet = "-999 in iter(mylist)"
def setup(size):
return "mylist = list(range(%d))" % size
start = time()
print("# Obj Size Time Obj Size Time")
for i in range(22):
size = 10*2**i # double in size each iteration.
setup_ = setup(size)
# As the size of the lists get bigger, and the time taken per test
# increases, we decrease the number of runs.
if size < 1000:
number = 200_000
elif size < 10_000:
number = 20_000
elif size < 100_000:
number = 2000
elif size < 1_000_000:
number = 200
else:
number = 20
print('%2d.' % (i+1), end=' ')
for name, snippet in [("list", list_snippet), ("iter", iter_snippet)]:
T = Timer(snippet, setup_)
best = min(T.repeat(number=number, repeat=7))
print(name, "%-8d" % size, "%10.4g" % (best/number), end=' | ')
print()
elapsed = time() - start
print("Total elapsed time: %f seconds" % elapsed)
I can only guess that there is a bug in your benchmarking code. It is impossible for searching an iterator to take constant time.
Perhaps you have forgotten that iterating over an iterator exhausts it? If you run item in myiter twice, the second time will take effectively zero time because the iterator is empty.
Exactly! It seems like a bug in the tool I am using. Below is my benchmark code:
import random
import perfplot
def setup(n):
data = list(range(n))
random.shuffle(data)
dict_array = {x:i for i, x in enumerate(data)}
return data, set(data), iter(data), dict_array
def list_in(*args):
return -99 in args[0]
def set_in(*args):
return -99 in args[1]
def iter_in(*args):
return -99 in args[2]
def dict_in(*args):
return -99 in args[3]
def convert_list_to_set(*args):
return set(args[0])
def convert_list_to_iter(*args):
return iter(args[0])
def convert_list_to_dict(*args):
return {x:i for i, x in enumerate(args[0])}
b = perfplot.bench(
setup=setup,
kernels=[
list_in,
set_in,
iter_in,
dict_in,
convert_list_to_set,
convert_list_to_iter,
convert_list_to_dict,
],
n_range=[2 ** k for k in range(1, 25)],
xlabel="length of the list.",
equality_check= None
)
b.show()
I reran the program. Now, the results change for convert_list_to_iter at the upper bound, which seems now to look as expected(converting a list into iter should be ~ O(1)). But the results for iter_in is completely wrong. You can refer to the results below:
I Even tried to benchmark the iter function alone. Yet, still showing the same results.
Now, I can confirm that it is indeed a bug in the tool I am using.
Hey @steven.daprano, it turns out that you have a little mistake in your code. You are taking into consideration the iter conversion. I have updated your code, now it looks like the following:
from timeit import Timer
print("# Obj Size Time Obj Size Time")
for iteration in range(25):
size = 10 * 2 ** iteration
if size < 1000:
number = 200_000
elif size < 10_000:
number = 20_000
elif size < 100_000:
number = 2000
elif size < 1_000_000:
number = 200
else:
number = 20
print(f"{iteration:.<2}", end=' ')
for name, snippet in [("list", "-99 in list_"), ("iter", "-99 in iter_")]:
T = Timer(snippet, (lambda n: f"list_ = list(range({n})); iter_ = iter(list_)")(size))
best = min(T.repeat(number=number, repeat=7))
print(f"{name} {size:<8} {(best/number):1.4g}", end=' | ')
print()
Which shows similar results as perfplot:
# Obj Size Time Obj Size Time
0. list 10 3.155e-07 | iter 10 7.538e-08 |
1. list 20 6.094e-07 | iter 20 6.584e-08 |
2. list 40 1.117e-06 | iter 40 7.547e-08 |
3. list 80 2.448e-06 | iter 80 8.883e-08 |
4. list 160 5.606e-06 | iter 160 8.822e-08 |
5. list 320 1.121e-05 | iter 320 8.999e-08 |
6. list 640 2.836e-05 | iter 640 1.032e-07 |
7. list 1280 5.062e-05 | iter 1280 9.029e-08 |
8. list 2560 8.867e-05 | iter 2560 9.425e-08 |
9. list 5120 0.0001777 | iter 5120 1.003e-07 |
10 list 10240 0.000392 | iter 10240 3.073e-07 |
11 list 20480 0.0007514 | iter 20480 3.129e-07 |
12 list 40960 0.001523 | iter 40960 9.238e-07 |
13 list 81920 0.004166 | iter 81920 1.902e-06 |
14 list 163840 0.007661 | iter 163840 0.0001409 |
15 list 327680 0.01217 | iter 327680 6.748e-05 |
16 list 655360 0.02328 | iter 655360 0.0001344 |
17 list 1310720 0.04645 | iter 1310720 0.002688 |
18 list 2621440 0.09363 | iter 2621440 0.005507 |
19 list 5242880 0.1998 | iter 5242880 0.0113 |
Do you have any explanation of what the iter function is doing at a low level? It behaves like a hashmap until a certain point(for a list of 1M items) ~O(1). I am looking forward to a response from a python core developer about what’s going on under the hood. What kind of magic is this?
You have repeated the same bug in your new version, which is why you are getting almost instantaneous results: your iterator is empty, so you are effectively searching iter([]) each time except for the first.
The timeit benchmarking class takes a statement to time, plus some setup code. The setup code is run once per run, then the statement is run over and over again, to average out any interference.
See the discussion by Tim Peters:
That was written many years ago, so some of the details are no longer relevent (timeit no longer uses either time.time or time.clock as the default timer), but it still gives you some idea of the difficulties in getting reliable timings.
But what matters here is that when the timeit.Timer class times a statement, it performs something like this:
run the setup code
initialise the timer
run the statement `number` times (defaults to 1 million)
finalise the timer
return elapsed time
The critical issue is that the setup code runs once per trial.
Let’s see what happens when you create an iterator once and then run
over it again and again:
values = iter([1, 2, 3, 4]) # Setup code runs once.
for n in range(5): # run the statement 5 times
print("3 is in values?", 3 in values)
When you run that, you will get this output:
3 is in values? True
3 is in values? False
3 is in values? False
3 is in values? False
3 is in values? False
What’s going on? Let’s simulate the in operator:
def my_in(target, container):
# Search for target in the container.
for value in container:
print(container, value) # see what we are looking at
if value == target:
return True
return False
values = iter([1, 2, 3, 4]) # Setup code runs once.
for n in range(5): # run the statement 5 times
print(my_in(3, values))
Run it and see if you can explain the output.
The critical issue is that you can’t iterate over an iterator twice
unless you re-initialise it. They are single-use only.
it = iter('abcd')
for letter in it:
print(letter)
# Do it again!
for letter in it:
print(letter)
print("Done.")
“Do you have any explanation of what the iter function is doing at a low level? It behaves like a hashmap until a certain point(for a list of 1M items) ~O(1).”
You are misinterpreting the data you have seen.
The canonical description of iterators comes from the PEP that introduced them:
but that site seems to be down right now. You can also read this:
https://docs.python.org/3/library/stdtypes.html#typeiter
The iter() builtin for lists works very roughly like this:
class Iter:
def __init__(self, values):
if isinstance(values, list):
self._hidden_state = values
self._counter = 0
else:
# Other types may be slightly different.
pass
def __next__(self):
if self._counter < len(self._hidden_state):
a = self._hidden_state[self._counter]
self._counter += 1
return a
raise StopIteration
(Aside: technically, the iter() builtin knows nothing about lists. It just delegates to the object’s __iter__ dunder, and it is list.__iter__ which knows how to handle a list.)
When you iterate over an iter() object, the interpreter simply calls the object’s __next__ method over and over again until StopIteration is raised. So for-loops look something like this:
# Simulate a for loop: for x in something: block()
it = iter(something) # May raise TypeError, if not iterable.
try:
while True:
x = next(something) # calls the magic __next__ dunder
block()
except StopIteration:
# End of the loop.
pass
When you iterate over a list or a tuple or string, the internal iterator gets consumed, but that’s okay, because it’s only internal and you don’t have direct access to it.
But when you iterate over an iterator you created yourself, it gets consumed as you use it, and if you want to iterate over it a second time, you have to re-create it.
So now let’s look at the in operator again.
When the iterpreter tries to execute x in something, it checks to see if something has the special __contains__ method (which lists do), and calls that. So lists, strings, tuples, dicts, sets etc can all have their own specialised method to implement in.
But if something is an iterator, it has no such specialised method, so
the interpreter falls back on the dumbest thing which can work:
for value in something:
if x == value: return True # Item is found!
return False # Not found.
And that iteration exhausts the iterator, eventually leaving it empty.
Aha! That’s why the search is almost instantaneous because the second time it searches for a value in the iterator, it throws a StopIteration exception. Now I get it. So, we simply can’t measure the average time it takes to look up an element within that iterator.
import time
list_ = list(range(10**3))
iter_ = iter(list(range(10**3)))
start = time.perf_counter_ns()
-99 in list_
end = time.perf_counter_ns()
print(end - start)
start = time.perf_counter_ns()
-99 in iter_
end = time.perf_counter_ns()
print(end - start)
Output
53603
86664
Never mind, the iterator is slower.
Besides, thanks for sharing these amazing resources.
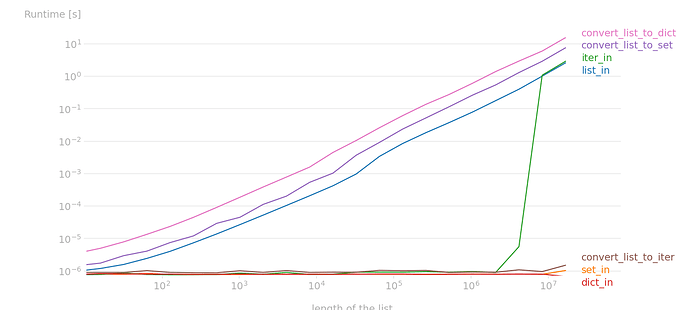
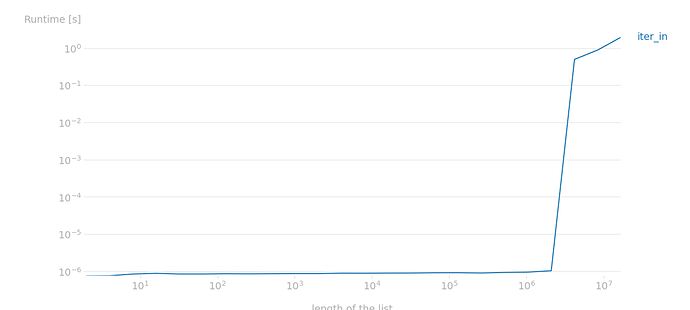
We can actually write a handy script to help us understand what timeit was trying to accomplish:
import time
list_ = list(range(10**3))
iter_ = iter(list(range(10**3)))
list_time_samples = []
iter_time_samples = []
for _ in range(100):
start = time.perf_counter_ns()
_ = -99 in list_
end = time.perf_counter_ns()
list_time_samples.append(end - start)
for _ in range(100):
start = time.perf_counter_ns()
_ = -99 in iter_
end = time.perf_counter_ns()
iter_time_samples.append(end - start)
print(sum(list_time_samples)/100, sum(iter_time_samples)/100, sep="\n")
print(iter_time_samples)
Output:
30687.56
1081.99
[53969, 629, 551, 573, 561, 539, 539, 644, 531, 544, 537, 516, 526, 548, 549, 539, 661, 539, 644, 581, 674, 534, 542, 531, 572, 536, 554, 586, 566, 707, 544, 700, 527, 546, 551, 536, 542, 553, 564, 534, 476, 514, 566, 1043, 511, 529, 514, 504, 499, 504, 509, 486, 507, 511, 516, 511, 509, 528, 509, 486, 506, 624, 506, 506, 546, 501, 516, 608, 524, 504, 509, 513, 508, 506, 586, 564, 511, 519, 682, 506, 572, 516, 557, 514, 514, 519, 596, 514, 624, 511, 521, 508, 516, 531, 544, 519, 514, 496, 514, 503]
That’s how timeit tricked me to make iter looks faster, it was measuring StopIteration all the time. Good to know! That sneaky little time watcher!
…but you can prepare multiple iterators in an iterable of iterators 
and measure the lookup time on them.
Sure we can, and I already did.
In practice, chances are that we should include the time needed to call iter(). Your data source is likely a concrete data structure like a list or a set, and we want to know whether converting it to an iterator will speed up searching. But to get an honest figure for that, we need to include the time it takes to make the iterator.
Only in the relatively unusual case that your data is already coming to you as an iterator would you want to exclude it.
But if you are worried about the overhead of calling iter() each time, we can adjust for that.
The overhead is approximately constant and small, so for large sequences of values, insignificant. We can measure that overhead and subtract it from the measured times.
Let’s take the worst possible case: searching a small list. What’s the smallest possible list? An empty list.
We can run timeit benchmarks from your shell’s command line (command.com or cmd.exe on Windows, or whatever terminal you use on Linux.)
python3.10 -m timeit "999 in []"
python3.10 -m timeit "999 in iter([])"
python3.10 -m timeit "iter([])"
and the output is:
20000000 loops, best of 5: 16.3 nsec per loop
5000000 loops, best of 5: 94.5 nsec per loop
5000000 loops, best of 5: 69.6 nsec per loop
So on my computer, it takes 16 nanoseconds to search an empty list.
(Actually, to be completely, pedantically precise, it takes 16 nanoseconds to create an empty list, and then search it.)
It takes 94 nanoseconds to do the same for an empty iterator, of which 70 nanoseconds is the overhead of calling iter() in the first place.
We can take that 70 nanoseconds as more or less constant, regardless of the size of the list. So if you find it takes one thousand nanoseconds (one microsecond) to search a larger iter(list), you can subtract 70 nanoseconds to get the time taken just in the searching part, without the overhead.
Of course all microbenchmarks should be taken as approximate. There is a fair amount of variability in the timing results, as the time will depend on what else the computer is doing, as well as the vagaries of CPU pipelines and code prediction.
Want to see something cool? Let’s compare the time to create, and then search, an empty list with the time taken to just create it:
[steve ~]$ python3.10 -m timeit "999 in []"
20000000 loops, best of 5: 16.3 nsec per loop
[steve ~]$ python3.10 -m timeit "[]"
10000000 loops, best of 5: 23.2 nsec per loop
I will be back in about 10 hours with the solution to this puzzle.
Interesting puzzle To me it looks like an optimization. Knowing that () is a singleton in CPython and checking the following…
~$ for code in "999 in []" "[]" "999 in ()" "()" ; do echo "$code" ; python3.10 -m timeit "$code" ; echo ; done
999 in []
10000000 loops, best of 5: 26.3 nsec per loop
[]
10000000 loops, best of 5: 22.5 nsec per loop
999 in ()
10000000 loops, best of 5: 26.4 nsec per loop
()
20000000 loops, best of 5: 11.9 nsec per loop
You got it! It’s an optimization.
When newer versions of CPython see you use a list in a way where there is no possible chance that it can be modified, or list methods called, the keyhole optimizer may replace it with a tuple instead.
Creating an empty tuple is cheaper than creating an empty list.