Numeric Generics - Where do we go from PEP 3141 and present day Mypy?

posita · July 7, 2022, 3:58pm

Inspiration: mypy/issues#3186. Please see that issue for a rich discussion and some very useful context and history. It’s long, but worth the time if you care about this issue. This post picks up from that thread.

I think solving this use case I identified in #3186 would go a long way:

I want to publish a library that does math on numeric primitives. I want to provide algorithms. I want my customers to be able to supply their own number implementations. I want to support typing annotations so that my customers can use existing tools to know whether their supplied number primitives satisfy interoperability requirements of my library. I also want to be able to check this at runtime in my library.

High bit: I think it’s important to define and enforce flavors of numerics as generic APIs. Builtin types should be compliant implementations.

At a high level, I think this involves:

Building something that allows for defining generic numerics and their operations. I’m pretty sure the consensus is that Mypy’s protocols are (currently) insufficient for this purpose.
Replace or simplify the numeric tower to comply with common operations (existing dunder methods seem reasonable). Establish explicit conversion/promotion APIs (both generic flavors and to builtin types). Minimize and explicitly and generically type implicit conversions like with __truediv__ and __pow__.
Bring both implementation and type definitions into compliance for all standard library primitives.

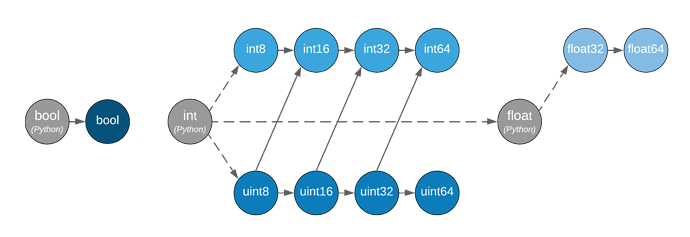
Mapping flavors onto a class hierarchy so far seems problematic, but it may be possible with care. I don’t think a class hierarchy should be a requirement. (I.e., we shouldn’t be afraid to ditch PEP3141.) Well-defined conversion/promotion APIs may suffice as an (albeit potentially complicated) alternative. I think the standard library is in a good position to define at least FloatT, RationalT, IntegerT (and maybe ComplexT), but if it does, builtin types (including Decimal and Fraction) should be compliant and should validate against those APIs.

I think achieving this in the standard library works benefits beyond just enabling generic algorithms to work with compliant numeric implementations. Additionally, it would act as a forcing function for internal consistency between numeric typing and numeric implementations. Further, it could role model techniques for third party math and science packages that promote interoperable extensions.

__truediv__ presents an oddity where an operator involving a single flavor (IntegerT) can result in a different flavor (IntegerT / IntegerT -> RationalT or IntegerT / IntegerT -> FloatT as it is currently). __pow__ presents additional sharp edges (IntegerT ** RationalT -> FloatT). Those and similar cases can probably be accommodated with care. @overloads may end up fairly complicated, but that may be an acceptable price to pay. Having clear lossy-vs-lossless conversion/promotion interfaces will likely help.

I don’t think it’s necessary to require interoperability between numeric implementations, but I think if you solve the above problem, you’ll get a lot of that anyway, especially if you enforce the presence of conversion/promotion interfaces like __float__, __trunc__, __int__, __floor__, __ceil__, etc. (maybe add __numerator__, __denominator__ with a default implementation for IntegerT, etc.). Numeric implementations could rely on Supports… interfaces to type and perform conversions/promotions before performing their operations. Or they could provide their own conversion/promotion implementations (e.g., sympy.sympify, which I believe is called implicitly to allow things like sympy.Symbol("x") + numpy.int64(0) to work). That being said, I think it’s really important that conversion/promotion APIs are clear when those are lossy vs. lossless. (SupportsInt for example is ambiguous. float.__int__ is potentially lossy. numpy.int64.__int__ is not.)

Jelle · July 7, 2022, 4:48pm

Thanks for starting this thread!

I’m not too sure about that. Have you explored using protocols for use cases like your generic numeric library? I feel like protocols should get you most of the way to what you want.

posita · July 7, 2022, 6:00pm

Protocols can’t have implementations, correct? I think we want static type checking to be consistent with (efficient) runtime checking, and Protocols don’t really do that well. I think that’s where ABCs make sense? I don’t think we need a hierarchy like the numeric tower, though. It may be that my Typing Fu is lacking. I’m not sure how Protocols and ABCs interact. Is something like this even possible?

from abc import abstractmethod
from typing import Protocol, TYPE_CHECKING

if TYPE_CHECKING:
    class FloatT(Protocol):
        def __init__(self, value: "FloatT" | "RationalT" | "IntegerT"): ...
        def __add__(self, other: "FloatT" | "RationalT" | "IntegerT") -> "FloatT": ...
        def __radd__(self, other: "FloatT" | "RationalT" | "IntegerT") -> "FloatT": ...
        def __float__(self) -> float: ...

    class RationalT(Protocol):
        def __init__(self, value: "RationalT" | "IntegerT"): ...
        def __add__(self, other: "RationalT" | "IntegerT") -> "IntegerT": ...
        def __radd__(self, other: "RationalT" | "IntegerT") -> "IntegerT": ...
        def __float__(self) -> float: ...
        def __numerator__(self) -> "IntegerT": ...
        def __denominator__(self) -> "IntegerT": ...

    class IntegerT(Protocol):
        def __init__(self, value: "IntegerT"): ...
        def __add__(self, other: "IntegerT") -> "IntegerT": ...
        def __radd__(self, other: "IntegerT") -> "IntegerT": ...
        def __float__(self) -> float: ...
        def __int__(self) -> int: ...
        def __numerator__(self) -> "IntegerT": ...
        def __denominator__(self) -> "IntegerT": ...
else:
    class FloatT:
        @abstractmethod
        def __add__(self, other: FloatT | RationalT | IntegerT) -> FloatT: ...
        @abstractmethod
        def __radd__(self, other: FloatT | RationalT | IntegerT) -> FloatT: ...
        @abstractmethod
        def __float__(self) -> float: ...

    class RationalT:
        @abstractmethod
        def __add__(self, other: RationalT | IntegerT) -> RationalT: ...
        @abstractmethod
        def __radd__(self, other: RationalT | IntegerT) -> RationalT: ...
        @abstractmethod
        def __float__(self) -> float: ...
        @abstractmethod
        def __numerator__(self) -> IntegerT: ...
        @abstractmethod
        def __denominator__(self) -> IntegerT: ...

    class IntegerT:
        @abstractmethod
        def __init__(self, value: IntegerT): ...
        @abstractmethod
        def __add__(self, other: IntegerT) -> IntegerT: ...
        @abstractmethod
        def __radd__(self, other: IntegerT) -> IntegerT: ...
        @abstractmethod
        def __float__(self) -> float: ...
        @abstractmethod
        def __int__(self) -> int: ...
        def __numerator__(self) -> IntegerT:
            return self
        def __denominator__(self) -> IntegerT:
            # This imposes a constraint on __init__, which is probably reasonable
            return type(self)(1)

class MyFloat(FloatT):
    def __init__(self, value: FloatT | RationalT | IntegerT): ...
    def __add__(self, other: FloatT | RationalT | IntegerT) -> "MyFloat": ...
    def __radd__(self, other: FloatT | RationalT | IntegerT) -> "MyFloat": ...
    def __float__(self) -> float: ...

class MyRational(RationalT):
    def __init__(self, value: IntegerT): ...
    def __add__(self, other: RationalT | IntegerT) -> "MyRational": ...
    def __radd__(self, other: Rational | IntegerT) -> "MyRational": ...
    def __float__(self) -> float: ...
    def __numerator__(self) -> "MyInteger": ...
    def __denominator__(self) -> "MyInteger": ...

class MyInteger(IntegerT):
    def __init__(self, value: IntegerT): ...
    def __add__(self, other: FloatT | Rational | IntegerT) -> "MyInteger": ...
    def __radd__(self, other: FloatT | Rational | IntegerT) -> "MyInteger": ...
    def __float__(self) -> float: ...
    def __int__(self) -> int: ...

integer_t_val: IntegerT = 0  # should validate
assert isinstance(0, IntegerT)  # needs to work at runtime
assert isinstance(0, RationalT)  # needs to work at runtime
assert isinstance(0.0, FloatT)  # needs to work at runtime
reveal_type(MyRational(0) + MyInteger(0))  # should yield MyRational
reveal_type(MyFloat(0) + MyRational(0))  # should yield MyFloat
reveal_type(MyInteger(0) + 0)  # should yield MyInteger
reveal_type(0.0 + MyFloat(0))  # should yield MyFloat

brettcannon · July 7, 2022, 7:30pm

Protocols are ABCs, so they can have an implementation and you can inherit from them. The key thing is they don’t have to be inherited from to signal they have been implemented to type checkers like ABCs.

posita · July 7, 2022, 8:58pm

So something like this?

from __future__ import annotations
from abc import abstractmethod
from typing import Protocol, runtime_checkable

@runtime_checkable
class FloatT(Protocol):
    @abstractmethod
    def __add__(self, other: "FloatT" | "IntegerT") -> "FloatT": ...
    @abstractmethod
    def __radd__(self, other: "FloatT" | "IntegerT") -> "FloatT": ...
    @abstractmethod
    def __float__(self) -> float: ...

FloatT.register(float)

@runtime_checkable
class IntegerT(Protocol):
    @abstractmethod
    def __init__(self, value: "IntegerT"): ...
    @abstractmethod
    def __add__(self, other: "IntegerT") -> "IntegerT": ...
    @abstractmethod
    def __radd__(self, other: "IntegerT") -> "IntegerT": ...
    @abstractmethod
    def __float__(self) -> float: ...
    @abstractmethod
    def __int__(self) -> int: ...

IntegerT.register(int)

class MyFloat(FloatT):
    def __init__(self, value: FloatT | IntegerT): ...
    def __add__(self, other: FloatT | IntegerT) -> "MyFloat": ...
    def __radd__(self, other: FloatT | IntegerT) -> "MyFloat": ...
    def __float__(self) -> float: ...

class MyInteger(IntegerT):
    def __init__(self, value: IntegerT): ...
    def __add__(self, other: FloatT | IntegerT) -> "MyInteger": ...
    def __radd__(self, other: FloatT | IntegerT) -> "MyInteger": ...
    def __float__(self) -> float: ...
    def __int__(self) -> int: ...

integer_t_val: IntegerT = 0  # should validate, but doesn't
assert isinstance(MyInteger(0), IntegerT)  # works because of registration
assert isinstance(0, IntegerT)  # works because of registration
assert isinstance(0.0, FloatT)  # works because of registration
assert isinstance(MyFloat(0), FloatT)  # works because of inheritance? not sure
reveal_type(MyFloat(0) + MyInteger(0))  # should yield MyFloat
reveal_type(MyInteger(0) + 0)  # should yield MyInteger
reveal_type(0.0 + MyFloat(0))  # should yield MyFloat

I think instance checks would have to be revisited if Protocols are to be used as ancestor classes. As of now, that check is not very efficient and imposes some odd behaviors that probably aren’t appropriate for direct inheritance.

I don’t know if something like this would suffice?

class _ProtocolMeta(ABCMeta):
    # …
    def __instancecheck__(cls, instance):
        if super().__instancecheck__(instance):
            # Short circuit for direct inheritors
            return True
        else:
            # … existing implementation that checks method names, etc. …
            return False

I’m not aware enough of all of the edge cases to know what problems the above would cause.

NeilGirdhar · July 8, 2022, 12:01am

Exactly. So I’m not sure why people want to use protocols here.

The main classes we want to inherit from the numbers ABCs are int, float, and complex. Whether these are manually registered in the typeshed or if they automatically inherit from a protocol doesn’t matter.

And the ABCs have some advantages. For a user-defined real number class, say MyReal, the user wants to ensure that MyReal inherits from Real. With a protocol, the user has to be exceptionally careful that interface matches the protocol’s interface. And if the protocol ever changes, MyReal’s definition has to change too. On the other hand, the ABC is registered and so the user is absolutely certain that the inheritance has happened.

Also, we already have the ABCs and some people are already using them.

I think if 2922 is implemented, the ABC registration of numbers seems like it will be a perfectly fine solution.

I think the central question that needs to be worked out is how to make the interface to the ABCs more meaningful than it is now. As Jelle pointed out, the typeshed has few annotations.

This probably needs an expert to work out the nuances, but I imagine something like:

class Real(Complex, SupportsFloat):
    @abstractmethod
    def __float__(self) -> float: ...
    @abstractmethod
    def __trunc__(self) -> int: ...
    @abstractmethod
    def __floor__(self) -> int: ...
    @abstractmethod
    def __ceil__(self) -> int: ...
    @abstractmethod
    @overload
    def __round__(self, ndigits: None | int = ...) -> int: ...
    @abstractmethod
    @overload
    def __round__(self, ndigits: int) -> Self: ...
    def __divmod__(self, other: Self | float) -> Self: ...
    def __rdivmod__(self, other: Self | float) -> Self: ...
    @abstractmethod
    def __floordiv__(self, other: Self | float) -> Self: ...
    @abstractmethod
    def __rfloordiv__(self, other: Self | float) -> Self: ...
    @abstractmethod
    def __mod__(self, other: Self | float) -> Self: ...
    @abstractmethod
    def __rmod__(self, other: Self | float) -> Self: ...
    @abstractmethod
    def __lt__(self, other: Any) -> bool: ...
    @abstractmethod
    def __le__(self, other: Any) -> bool: ...
    def __complex__(self) -> complex: ...
    @property
    def real(self) -> Self: ...
    @property
    def imag(self) -> float: ...
    def conjugate(self) -> Self: ...

Or maybe these functions should accept any Real, and call float if they need to?

posita · July 8, 2022, 1:32am

And Fraction and Decimal, since those are number-like things in the standard library. And possibly bool, if it is to continue possessing number-like characteristics on its own (though I don’t think this is a requirement; bool could be limited to numerics’ operator arguments without a full set of integer operators on its own). I’m not sure what we do with things like IntEnum.

Noted and thanks for the example and reference. I’m not sure Self carries this across the finish line, though. I’ll start tinkering with 3.11.

My instinct is that defining numeric APIs through composition (e.g., via Supports… mix-ins and possibly other implementation mix-ins) rather than strict inheritance is the way to go, but we can explore that. SupportsIndex already captures the concept of lossless conversion to int, so that’s already present.

This is likely a bigger question that requires further discussion. I can see standard library primitives implementing something with regards to other standard library primitives, but there should probably be a mechanism that allows third parties to prioritize their own promotions/conversions. For example, it would be weird if numpy.int64 / Fraction resulted in a numpy.float128, but Fraction / numpy.int64 resulted in a Fraction or float. I don’t know how this gets captured via type annotations.

posita · July 8, 2022, 9:08pm

Responding in part to @mdickinson via python/mypy#3186:

I’d love to see proposals for a reworked numeric tower based on typing use-cases; I don’t have a huge amount in the way of time and energy to offer, but would be willing to sponsor a PEP, or at the very least to review a PEP authored / sponsored by others.

I would love to get to this point, too. If I can carve out time, and if others are willing to provide patience and guidance (with tolerance of my being slow, but I’ll definitely try to get there eventually), I am willing try my hand at this. (Others should not be dissuaded from doing the same. I understand that pesky day jobs have a tendency to get in the way.)

Trying to mutate or adapt the existing numbers module to fit the needs of the typing community seems like a much harder proposition, not least because published interfaces are horribly rigid (add anything new and you break implementers of that interface; remove anything and you break the users). I don’t see a strong need to deprecate PEP 3141; I’d just accept that it’s not all that useful for typing purposes, ignore it and move on.

I think it’s at least important to signal to newcomers via the most popular surface (i.e., the standard library documentation) that PEP 3141 is not a typing system. That’s currently unclear, and those who don’t monitor mailing lists, GH issues, etc. can easily mistake it for one and then spin their wheels for a long time trying to get it to work as one. But, as you point out, we don’t have to reach that decision until we’re confident in a viable alternative, so first things first, which I think is just a less clear way of restating your proposed next steps.

I think there’s a set of really hard problems to do with mixed-type arithmetic that it may not be reasonable to expect any kind of typing framework to solve. Suppose I have two different Real-like classes A and B; there are all sorts of ways that mixed-mode arithmetic between A and B, A and float, B and int, etc. might work or not work; it may simply not be reasonable to try to capture all of the possible permutations in type declarations. (For an example of how not to do it, take a look at the GAP framework. But this at least demonstrates that there’s a hard problem to solve.)

I don’t think ubiquitous inter-implementation operator interoperability should be a requirement. For example, I don’t think the standard library should impose support for all math operations between numpy.int64 and sage.rings.real_mpfr.RealNumber as a condition of participation of either. One shouldn’t prevent authors of one or both of those from explicitly supporting each other, but requiring it of them seems unreasonable.

I do think it’s worthwhile to target use cases where one could say, “Give me your interoperable implementations of Float, Rational, and Integer, and I’ll perform this algorithm using those primitives.” That might converge to the same problem, but at this point, I’m hopeful it’s simpler. Maybe requiring that implementations are interoperable with standard library primitives is good enough? Dunno.

FWIW, I’ve done a fair amount of numeric coding both at home (mostly number-theoretic or concerned with esoteric floating-point stuff) and at work (mostly data-science’y and based on the standard NumPy / SciPy / tensorflow / … scientific stack), and in the time since the numbers module was brought into existence I have yet to find it useful. What has been useful are typing protocols like SupportsIndex and SupportsFloat. (SupportsInt, not so much.) The kind of use-cases I personally have, and would love to see addressed in any new proposal, are things like “usable as a float”, “usable as an int”, “can be converted to a Fraction”.

I probably don’t have nearly the exposure you do, but my experience echoes yours. Maybe Supports… is the way one gets to standard library interoperability?

mdrissi · July 9, 2022, 8:03am

This discussion reminds me of the array api and question of what is an array? Being able to interchange numbers is useful, but is very closely related to interchanging arrays of numbers like tensorflow tensors, numpy array, pytorch tensors, cupy tensors, etc. Python array API standard — Python array API standard 2021.12 documentation documents array api standard which roughly is trying to define common collection of methods present in each array related library and standardizing signatures. I think it would be valuable to have feedback from the participants of that work and it’d be sad if new number type system wasn’t used as primitives for array types. @rgommers

I like SupportsFloat/SupportsX approach and just have more protocols like,

class FloatLike(Protocol)
  # Or just use __float__ but not all number likes have dunders today. 
  # Or maybe add __decimal__/__fraction__/etc dunders?
  def to_float(self) -> float:
    ...

class IntLike(Protocol):
  def to_int(self) -> int:
    ...

class FractionLike(Protocol):
  def to_fraction(self) -> Fraction:
    ...

# Similar for decimal/complex/etc.

and then expect that libraries specify which XLike things they work with and can call conversion themselves at beginning. That’s roughly tensorflow’s approach for tensor likes where any class that has tf_tensor method + some basic types are considered tensors. Most tensorflow functions start with tf.convert_to_tensor(tensor_like).

Alternative approach of SupportsAdd, SupportMult is fine too although there’s awkward trade off of supporting too few things makes it challenge to use it, but if you support 20 operations (plus, minus, negate, divide, multiply, pow, floor, …) you may exclude stuff too easily. I think for that route we’d have collection of basic protocols + subclasses/intersections of common groups.

The main awkward thing with SupportsAdd approach is what exactly are input/output type rules? int + int = int is nice and normally for any “numeric” type T + T = T. But what about S + T where S/T are different numeric types? Output rules for numerics are a mess and even different array libraries are inconsistent on how two numbers of different types combine. Is S + T always same type as T + S? I hope that’s true but not even sure. I’d be happy to pretend that’s true though and consider non-commutative type rules not worth complexity.

uhasker · July 9, 2022, 9:43am

As far as I can see there are the following approaches currently under discussion:

Approach No. 1:

Just clean up the current number tower by e.g. dropping the Number class, fixing the interfaces etc. Since @posita already outlined a lot of stuff in that regard, I won’t repeat it here.

Approach No. 2:

Forget about the number tower & focus on SupportsInt, SupportsFloat etc. Then the respective code would need to convert to int & continue dancing from there (if I understand this correctly). Since we are trying to talk about real use cases, I’ll just pull out the one that led me to the mypy issue & this discussion:

class SomeClassWithADict:
    def __init__(self, d: Dict[Integral, Integral]):
        self.d = d

This would then become

class SomeClassWithADict:
    def __init__(self, d: Dict[SupportsInt, SupportsInt]):
        self.d = {int(k), int(v) for k, v in d.items()}
        # the cast could also possibly happen at some other point

Approach No. 3:

Exploring that idea (hey, you asked :)), it might be interesting to think about defining Field, Ordered etc which would look something like this:

class Field:
    def __add__(self): ...
    def __sub__(self): ...
    def __mul__(self): ...
    def __div__(self): ...
    ...

class Ordered:
    def __lt__(self): ...
    def __gt__(self): ...
    def __eq__(self): ...

Then we could do stuff like:

class OrderedField(Field, Ordered): ...

Basically this would be an attempt to reproduce the respective algebraic structures. Note of course that the code above is just a stubby example (and as we already noted in the mypy issue, actual floats don’t form a field) - the point is not the code, but the idea.

This sounds very nice in theory (to me at least), but of course this would be very complicated both to create & understand. In addition PEP3141 tried something like this (see the “Rejected” section) & it didn’t seem to work. Still I think it’s useful to keep this in mind as a source of inspiration.

I probably missed something, so don’t hesitate to correct to/add to this list (I just wanted to start collecting solutions).

Probably the way to go is to (as @mdickinson pointed out) centrally collect the use cases somewhere, centrally collect possible solutions somewhere, write a bunch of documents outlining each approach to a certain reasonable degree & go from there.

rgommers · July 23, 2022, 8:42pm

Regarding the array API standard and “types of numbers” (or “dtypes” in numpy or array/tensor libraries in general): this is somewhat related to the use case that @posita started with, but the dtypes are quite different. For numeric/scientific computing and ML/AI use cases, the key topics are:

What are the relevant dtypes?
What are the type promotion rules between them.

The answer to (1) is: (a) Python builtins bool, int, float and complex, and (b) corresponding fixed-size numerical dtypes: (u)int8 ... (u)int64, uint8 ... uint64, float32, float64, complex64, complex128. What is of most interest beyond that is lower-precision dtypes (float16, bfloat16, float8, int4 for deep learning in particular). long double is basically dead. When we look at dataframes instead of arrays, we can add that string dtypes, categoricals and datetimes are important. A fixed-point dtype (equivalent to Decimal) may be relevant for dataframes because it has applications in finance. The other numerical types in the stdlib (Fraction, Decimal) are not very interesting; numpy has spotty support for them via the object dtype, no other array libraries will work with them. long double is no longer useful either (a proper 128-bit floating point dtype would be for scientific computing, but it does not exist in any library).

The answer to (2) is (from Type Promotion Rules — Python array API standard DRAFT documentation):

I’m not sure if whatever may replace the numeric tower can somehow interoperate with that type promotion structure, but if that replacement is to be relevant, it probably should. The point made in the first post on this thread about distinguishing between lossless and lossy promotions matters here.

This I agree with. When you try to mix numerical types that don’t know about each other, it’s extremely difficult to get well-defined behavior without corner cases. It’s often better to just error out and let the user do an explicit conversion. For array libraries we use a similar principle: a key goal is to write code in array-consuming libraries (e.g., scikit-learn) that works with any array library, however array libraries only have to provide primitives that work with their own array type. Code like numpy.add(x1_numpy, x2_pytorch) is error-prone. Best to error out and not let the user convert explicitly to the output type they want to obtain.

That’d be my instinct as well. Let me add that, for , NumPy has a class hierarchy (both old, see NEP 40 and new/redesigned, see NEP 42), but it’s not necessary and other array libraries typically don’t use a class hierarchy.

it’d be sad if new number type system wasn’t used as primitives for array types

Let me circle back to this: I read this as a runtime thing, which I don’t think this will happen (we’ve got basically what we need in the promotion diagram above). What is useful and we’d happily adopt though is improved type annotation support. In the array API standard we haven’t had too many issues with static typing, because it’s a new project - Protocol for array objects · Issue #229 · data-apis/array-api · GitHub is the most relevant open issue. NumPy was much hairier; it does now have fairly complete type annotations (thanks to a heroic effort from Bas van Beek). It uses SupportsInt|Float|Index|Complex in places, those have been useful. Looking at the existing `.pyi files in NumPy may yield some insights about what’s needed or can be simplified.

oscarbenjamin · July 23, 2022, 11:41pm

When you get far enough into trying to write generic code for different implementations of numbers or rings and fields what you’ll find is that you basically always need to know a few properties about the kind of ring/field/number you are dealing with to be able to write the proper code. In other words nontrivial code cannot be completely generic. The problem with the numbers ABCs is that apart from Integral and Rational they don’t provide any information to be able to do anything useful except in very simple situations.

For example in the case of Real if I have a Real that is not a float then what could it be? It might be one of the np.float32 etc types that @rgommers referred to above or it might be:

Decimal (assuming Decimal was allowed)
mpmath.mpf (an arbitrary precision binary float)
sympy.Float (an mpmath.mpf with an attached measure of accuracy)
An interval (or ball) from an interval arithmetic library.
An element of the algebraic field Q(sqrt(2)) as provided in SymPy/SageMath and others.
A more complicated symbolic representation of an exact real number.

None of the above can in general be handled by the same generic code unless you are doing something extremely simple. Projects like SymPy and SageMath that have lots of different types like this will have associated “context” or “domain” objects that are used for keeping track of which kind of field/number is being represented and how to implement things that need non-generic implementations.

That’s not to say that there can’t be generic code for these. The problem is that nontrivial generic higher-level code will need to call into some non-generic lower-level routines. The numbers ABCs don’t provide enough of a usable foundation for the code above them to be generic without being highly suboptimal.

A simple example would be a function that takes Real and returns some calculated result where the calculation needs to do more than basic arithmetic such as computing the exponential exp(x) of one of its arguments. There is no extensible way to do that in Python that will perform correctly for ordinary floats and at the same time 1000 digit mpmath.mpf floats (where you care about the 1000 digit accuracy). The ABC only defines __float__ and therefore you can use math.exp but it will reduce your 1000 digits to 53 bits.

Likewise nontrivial usage of Decimal that actual needs the important decimal-ness of Decimal probably needs to know that it is using Decimal so that it can set up a context and set rounding modes and precision and so on. Nontrivial usage of mpmath needs to set the precision and needs to use the mpmath functions for sin, cos, exp etc. The only thing that the Real ABC provides for interoperability is __float__ but the whole point of saying Real rather than float is because you want to handle more than float and the whole point of using mpf/Decimal is that they are better than float in some ways: converting everything to float with __float__ misses the point of using the other types in the first place.

The ABCs don’t give any way to know that any operations will be exact or not but that distinction typically leads to completely different algorithms. Likewise in some fields or rings some operations will be unknowable or undecidable which also leads to completely different algorithms. No information is provided by the ABCs that would enable exact conversions even between different floating point types (__float__ doesn’t cut it and neither does as_integer_ratio).

I would like to see better interoperability of different numeric types in Python. I think that making type annotations the primary focus of that is misguided though. We really need to improve the actual semantics and usefulness first and think about typing after. I worry that some of the people in the mypy issue are just looking for a way to hint all their code and shut up mypy and perhaps don’t really have a clear application for why they even need to use the ABCs in the first place. It would be a shame to solve their problem the easy way without actually improving anything useful.

One thing that I think would be a big improvement for generic numeric code would be a stdlib version of the math module that had overloadable singledispatch functions for common mathematical operations like sin, cos, etc. Then you could do something like sin(obj) and have it do the right thing for every type of obj. Then you could use that in a generic routine instead of needing to choose from math.sin, cmath.sin, numpy.sin, mpmath.sin, sympy.sin, … These could be used recursively so e.g. a numpy array with dtype=object could use the single dispatch sin to operate on its elements. (Note that this is exactly how it works in Julia - one sin function overloaded by different types.)

cfcohen · July 24, 2022, 6:11pm

I agree strongly with practically everything Oscar said in his most recent message. I reject the argument that Fraction and Decimal “are not very interesting”. In particular, I’ve become quite enamored with the perfect precision that Fraction and arbitrarily sized integers provides for certain classes of problems. I definitely want more than annotations to just “shut up mypy”. I want a robust definition of the Numeric tower that includes concepts like Fields and Ordering. I want to know which operations each class in the Numeric tower are required to support. I want to track the precision of various operations and to be able to tell whether I’ve lost precision or not.

As an example of my use case, imagine that I want a geometric library that calculates the properties of various shapes and solids. I’d like to be able to calculate the area of a square with an integer or fractional side, and return a perfect precision answer as an integer or fraction. When calculating the area of a circle things are more complicated (because of those darn transcendental numbers), but I’d like to do something to get an answer, even if it’s to downgrade precision to a float. Hopefully, it’s easy to see that tracking the types given different inputs gets very complicated very quickly, and thus the need for mypy to help manage that complexity. I want to invoke the same routines with sympy symbols, and get back the formula for the area.

My problem domain has largely been focused on getting math in Python to behave like I was taught in grade school (e.g. 0.1+0.1+0.1=0.3, not 0.30000000000000004), so as to avoid the kinds of bugs that result from floating point errors. That said, I recognize that floating point calculations often perform “a little bit better” than say arbitrary precision Fractions or sympy, and would like to retain the ability to invoke the same code in the floating point domain.

Oscar’s commentary on unified support for trigonometric functions across several math domains is exactly what I’ve done, along with a passable implementation of several features like the geometry example above. I’ve also changed a few things about Fraction and Decimal and their relationships with the rest of the system that I think was ill-advised. I implemented algorithms to compute π and e to arbitrary precision in the rational domain, so that touching transcendental numbers doesn’t immediately result in downgrading to float precision in the Fraction domain. My most troublesome problem has actually been the inability to override Python’s default behavior of int / int -> float, which I would prefer to have returned a perfect precision Fraction (at least in this case). I’ve been able to work around this limitation by careful conversion of ints to Fractions whenever division occurs.

In summary, I’d like for the new Numeric tower to be sufficiently descriptive that we can actually unify all of these disparate math libraries and make it possible to write reliable code that works correctly across various implementations. I’d like for mypy to be able to reason correctly about what inputs to which math functions result in which types, in that very messy environment. And I’d like for those types to not be gigantic Unions of all supported implementations, but something more principled like Number.Rational.

I realize that there are a lot of “I want” and “I’d like” in this post. My goal was simply to document what my use case is, and support the argument that mypy type checking is just part of the problem. In my opinion, it would be very sad to just give up on the Numeric tower completely.

posita · August 21, 2022, 5:45pm

I’ve been thinking about this casually for a few weeks, and have a few additional thoughts. First, I think I am echoing @oscarbenjamin’s (and others’) sentiments when I say that type-checking is an increasingly valuable (and expected) feature of interfaces. This is subtle, but (I think) is best highlighted by library authors. In effect, those authors are beholden to the limitations of the language/standard tooling, but they produce a product whose audience is comprised of other developers. An increasingly important feature of that product is type-checkable APIs.

Second, I think it would be useful to identify a few use cases that would serve both to ground conversations, but also to more concretely define the boundaries of any solution and may serve to fight through some of the fog.

Third, I do not think it should be within the purview of the standard library to allow the “generification” of arbitrary mathematical concepts. I think higher level computations are properly left to proprietary library interfaces. I think we already have a pretty good hint at what can (or perhaps should) be supported, which maps nicely to existing operator dunder methods, which could be augmented as necessary (e.g., with something akin to __numerator__, __denominator__, etc.).

Taking arrays as inspiration, I propose the following mental exercise. Let’s say you want to author a generic sequence of uniform numerical primitives (let’s call it NumSequence), somewhat akin to list[T] (where T is some kind of TypeVar). You want to support dunder operations to the extent that T supports them with the following semantics:

NumSequence <binop> <scalar> should result in a new NumSequence whose items consist of <binop> being applied to each item in the original NumSequence and <scalar>.
NumSequence <binop> NumSequence should result in a new NumSequence whose items consist of <binop> being applied to the Cartesian product of each item in each of the two original NumSequences.
If <binop> is unsupported between the various operands, it should fail at runtime with a TypeError and should raise a warning during type-checking.

We want something like the following:

reveal_type(numpy.int32(1) / numpy.int32(1))  # numpy.float32
num_seq = NumSequence(numpy.int32(i) for i in range(10))
reveal_type(num_seq)  # NumSequence[numpy.int32]
reveal_type(num_seq / numpy.int32(1))  # NumSequence[numpy.float32]
reveal_type(num_seq / "Hey!")  # Any w/ error

Instantly, we can see issues arise. For example, we can implement NumSequence.__truediv__ to return NotImplemented where unsupported operands are discovered at runtime. However, signaling that during a type-checking phase isn’t possible without exhaustive enumeration of all known types and their combinations (at least as far as I know).

As far as I know there’s no way to say something like, “If operands support multiplication among themselves, then I support it and will adopt the type of whatever they fine as the result type, but if they don’t, then I don’t.” I think that’s likely a good proxy for the problems we’re trying to solve. If we had some Protocol-like mechanism for describing that, getting out of the business of defining a number hierarchy becomes far easier, as consumers can describe what they need and what they produce in terms of individual operations.

One stumbling block is envisioning what that looks like in syntax. How could one describe a function that: takes a first generic argument of T1; takes a second generic argument of T2; and produces a result based on an inferred result type of __truediv__(T1, T2) (which could be NotImplemented)?

bradd · December 8, 2022, 11:24am

Fraction/Rational are important for applications like discrete probability analysis, for example. I’m working on just such a project, which ultimately led me down the numeric typing rabbit hole and into this discussion. Currently I’m working with values that are sometimes probability mass functions, but usually they’re just integers or fractions (so basically Union[int, Fraction, pmf]). It’d be handy if I could easily arrange those into a type hierarchy with a common root, but as @cfcohen noted above we don’t even have intuitive behavior for interactions between the standard int and Fraction types.

It’s possible that my best option is to just model the rational values as corner cases of the pmf type (i.e., a rational is just a single-valued pmf with probability 1). Or I could do something with duck typing and give up on static type analysis, although I’d prefer to design something reusable with meaningful type hints, as I’m hoping to make a reusable library. Even ignoring the complications of the pmf, it would help if Python had more intuitive Rational support, and even better if the numeric types were easier to extend.