I have looked everywhere and I can write a summation in python (I think) but I do not know how to find the upper limit of a summation.
The example question I have is shown in the image below:
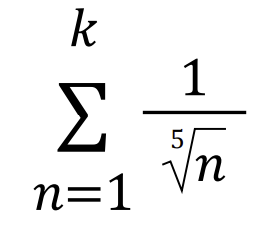
This is equal to 511.
Thank you!
I have looked everywhere and I can write a summation in python (I think) but I do not know how to find the upper limit of a summation.
The example question I have is shown in the image below:
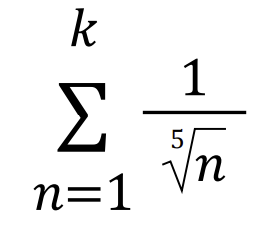
This is equal to 511.
Thank you!
k is undefined here. Is your task to find the value for k such that it equals 511? Otherwise I am not sure what you are asking.
Yes, sorry for not being clearer, it is.
First observation: the summation is only defined for whole-number values of k, and it won’t be equal to 511 for any k - it will go from being a bit less, to a bit more. (A priori, it’s a miracle if we sum a bunch of irrational numbers and get an integer out of it; but also I tried actually checking the values. The first value above 511 is in fact slightly above 511, something close to 511.0038.) Of course, a corresponding integral could give us a k value where the definite integral has a value of 511 exactly; but solving a problem like that is far more complex (and also not what’s being asked).
It’s hard to suggest a modification to your existing code without seeing it (assuming you wrote some - if you’ve only thought about the problem, that’s also fine). So, I assume that you’re just looking for a general hint to approaching the problem.
I assume you already figured that some kind of loop should be involved in the Python code, to add up terms one at a time. Try checking the value that you got “so far” after adding each term, and seeing what the value of k is once the target value of 511 has been exceeded.
There isn’t really a direct, general approach to this. There are tricks you could try like doing a “binary search” for a k value that works, but they don’t really actually help (because you still have to add up all the terms from 1 to k to check the result). That sort of thing can only help if you can find a closed form for the summation (which is a math problem, not a programming problem).
Hi,
I re read the question and it is to find the value of K such that the whole summation is greater than or equal to 511 (obviously not equal to).
I do not have a clue on where I would even start on python - I’m really really struggling with all coding.
What resources does your course offer?
Are you expected to learn basic python?
Have you read any python tutorials?
If not maybe start with a tutorial.
You’re looking for a k such that, that sum equals to 511 exactly, which it won’t. The terms of your sum will never be whole integers except for n = 1. You can certainly evaluate such sums in Python for particular integer values of k and by interpolation figure out what the “real” k should be.
>>> sum(1 / math.pow(n, 1/5) for n in range(1, 1841))
510.7814294950361
>>> sum(1 / math.pow(n, 1/5) for n in range(1, 1842))
511.0037549769149
Unless I’m mistaken, I think you’re dealing here with partial sums of the Riemann zeta function for s = 1/5 (as your sum is just 1/1^(1/5) + 1/2^(1/5) + ... + 1/k^(1/5) for values of k. This mathoverflow post may also be useful.
P. S. If you’re new to Python, note that range(m, n) will be the sequence of numbers m, m + 1, ... n - 1. So range(1, 1841) is the sequence 1, 2,...,1840 and range(1, 1842) is the sequence 1, 2,...,1840, 1841. So if you’re looking for a smallest k such that the sum above >= 511 then it’s 1841. Make a function out of the expression above, with k as a variable, and experiment with values of k.
You could also consider a mathematical package like Mathematica.
CORRECTED: series diverges: as k approaches infinity the denominator of each term approaches infinity and the reciprocal approaches 0, slower than harmonic series (1/1 + 1/2 + ... 1/n).
Correct result, wrong argument. The denominators do approach infinity, and the reciprocals do approach 0, but they are just too slow, specifically n ^ (1/5) is slower than n, which means this is slower than the harmonic series and therefore the series diverges.
Yes, you’re right. Convergence occurs if Re(s) > 1.
You could use Sympy here:
>>> from sympy import symbols, Pow, summation
>>> n = symbols('n', integer=True)
>>> expr = summation(1 / Pow(n, 1/5), (n, 1, oo))
>>> expr
Sum(n**(-0.2), (n, 1, oo))
>>> expr.limit(n, oo)
Limit(Sum(n**(-0.2), (n, 1, oo)), n, oo, dir='-')
It can’t evaluate that limit as the sum diverges, so it gives you simply an expression.