How is the covariance scaled when the scale_covar parameter is set to True in a call to lmfit.minimize(...)

[elivesay2000 (Eric Livesay)]

Hi.

I’ve recently encountered the fact that the covariance matrix can be scaled or unscaled when a minimization is performed using the Levenberg Marquardt Method lmfit.minimize(…). How is the scaling performed?

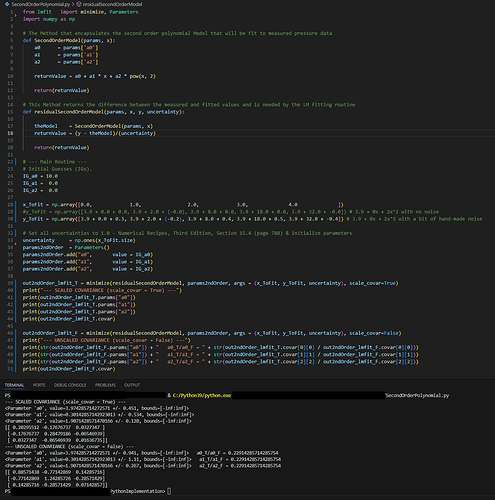
An example of this is found in the code below which fits a second order polynomial of the form y = a0 + a1x + a2x^2 to 5 points. The covariance matrix for the fit is different depending on whether the scale_covar pamameter is set to True (T) or False (F). However, the ratio of the diagonal elements is the same for elements [0][0], [1][1] and [2][2] (i.e., 0.22914285… in the attached screenshot). How is this scaling factor calcluated?

Thanks,
Eric

from lmfit   import minimize, Parameters
import numpy as np

# The Method that encapsulates the second order polynomial Model that will be fit to measured pressure data
def SecondOrderModel(params, x):
    a0      = params['a0']
    a1      = params['a1']
    a2      = params['a2']

    returnValue = a0 + a1 * x + a2 * pow(x, 2)

    return(returnValue)

# This Method returns the difference between the measured and fitted values and is needed by the LM fitting routine
def residualSecondOrderModel(params, x, y, uncertainty):

    theModel    = SecondOrderModel(params, x)
    returnValue = (y - theModel)/(uncertainty)

    return(returnValue)

# --- Main Routine ---
# Initial Guesses (IGs).
IG_a0 = 10.0
IG_a1 =  0.0
IG_a2 =  0.0

x_ToFit = np.array([0.0,             1.0,                2.0,             3.0,              4.0              ])
#y_ToFit = np.array([3.9 + 0.0 + 0.0, 3.9 + 2.0 + (-0.0), 3.9 + 8.0 + 0.0, 3.9 + 18.0 + 0.0, 3.9 + 32.0 + -0.0]) # 3.9 + 0x + 2x^2 with no noise
y_ToFit = np.array([3.9 + 0.0 + 0.3, 3.9 + 2.0 + (-0.2), 3.9 + 8.0 + 0.4, 3.9 + 18.0 + 0.5, 3.9 + 32.0 + -0.4]) # 3.9 + 0x + 2x^2 with a bit of hand-made noise

# Set all uncertainties to 1.0 - Numerical Recipes, Third Edition, Section 15.4 (page 788) & initialize parameters
uncertainty     = np.ones(x_ToFit.size)
params2ndOrder  = Parameters()
params2ndOrder.add("a0",       value = IG_a0)
params2ndOrder.add("a1",       value = IG_a1)
params2ndOrder.add("a2",       value = IG_a2)

out2ndOrder_lmfit_T = minimize(residualSecondOrderModel, params2ndOrder, args = (x_ToFit, y_ToFit, uncertainty), scale_covar=True)
print("--- SCALED COVARIANCE (scale_covar = True) ---")
print(out2ndOrder_lmfit_T.params["a0"])
print(out2ndOrder_lmfit_T.params["a1"])
print(out2ndOrder_lmfit_T.params["a2"])
print(out2ndOrder_lmfit_T.covar)

out2ndOrder_lmfit_F = minimize(residualSecondOrderModel, params2ndOrder, args = (x_ToFit, y_ToFit, uncertainty), scale_covar=False)
print("--- UNSCALED COVARIANCE (scale_covar = False) ---")
print(str(out2ndOrder_lmfit_F.params["a0"]) + "   a0_T/a0_F = " + str(out2ndOrder_lmfit_T.covar[0][0] / out2ndOrder_lmfit_F.covar[0][0]))
print(str(out2ndOrder_lmfit_F.params["a1"]) + "   a1_T/a1_F = " + str(out2ndOrder_lmfit_T.covar[1][1] / out2ndOrder_lmfit_F.covar[1][1]))
print(str(out2ndOrder_lmfit_F.params["a2"]) + "   a2_T/a2_F = " + str(out2ndOrder_lmfit_T.covar[2][2] / out2ndOrder_lmfit_F.covar[2][2]))
print(out2ndOrder_lmfit_F.covar)

[kknechtel (Karl Knechtel)]

lmfit isn’t a major library, so people aren’t necessarily going to know how it works (it isn’t even on GitHub so I can’t use the “stars” count there to measure popularity). That said, it sounds like you really have a question about the mathematical theory, rather than actually about programming… ?

[jagerber (Justin Gerber)]

lmfit is a pretty well used library in the scientific community. Here’s the github page. It would be most appropriate to ask this question as a Q&A question in the discussion section there.

[elivesay2000 (Eric Livesay)]

Thanks Justin. That github page was exactly what I needed.

In particular, the page titled fitting.rst had details about the scale_covar parameter that led to the fact that the scaling factor being used was the reduced chi-squared statistic. I’ve also added some details about the value of the reduced chi squared statistic from my example (taken from the scale_covar = False data) in case anyone comes along with the same question and wants more details.